Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
orthProj
Computes the orthogonal projection of a point to a polyline in the plane.
Syntax
[d,ptp,ind,c] = orthProj(data,pt)
Arguments
- data
a n by 2 array. The first column contains the X coordinates of the polyline, while the second one contains the Y coordinates.
- pt
an array with 2 entries: the coordinates of the point
- d
The minimum distance between the given point and a polyline data point.
- ptp
an array with 2 entries: the coordinates of the point that realizes the minimum distance
- ind
The polyline closest point lies on the segment
[ind ind+1].- c
The interpolation coefficient of the orthogonal projection.
Description
Computes the orthogonal projection of a point to a polyline in the plane.
Examples
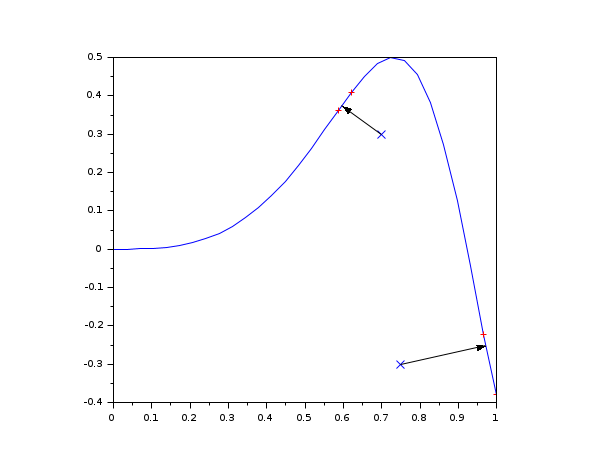
x=linspace(0,1,30)'; y=sin(4*x.^3)/2; clf(), isoview() plot(x,y) pt=[0.7 0.3]; plot(pt(1),pt(2),'xb') [d,ptp,ind,c]=orthProj([x y],pt); plot(x(ind:ind+1),y(ind:ind+1),'+r') xpoly([pt(1);ptp(1)],[pt(2);ptp(2)]) e=gce();e.polyline_style=4;e.arrow_size_factor = 1.5; pt=[0.75 -0.3]; plot(pt(1),pt(2),'xb') [d,ptp,ind,c]=orthProj([x y],pt); plot(x(ind:ind+1),y(ind:ind+1),'+r') xpoly([pt(1);ptp(1)],[pt(2);ptp(2)]) e=gce();e.polyline_style=4;e.arrow_size_factor = 1.5;
See Also
- proj — projection
- householder — Householder orthogonal reflexion matrix. Symetrical wrt a plane
- scaling — affine transformation of a set of points
| Report an issue | ||
| << move | transform | rotate >> |