Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
ndgrid
build matrices or N-D arrays by replicating some template vectors
Syntax
[X, Y] = ndgrid(x) [X, Y] = ndgrid(x,y) [X, Y, Z] = ndgrid(x,y,z) [X, Y, Z, T] = ndgrid(x,y,z,t) [X1, X2, ..., Xm] = ndgrid(x1,x2,...,xm)
Arguments
- x, y, z, ...
vectors of any data types. They may have distinct data types. By default,
y=x.- X, Y, Z, ...
matrices in case of 2 input arguments, or hypermatrices otherwise. They all have the same sizes:
size(x,"*")rows,size(y,"*")columns,size(z,"*")layers, etc. They have the datatypes of respective input vectors:typeof(X)==typeof(x),typeof(Y)==typeof(y), etc.
Description
The first application of ndgrid is to build a grid of nodes meshing the 2D or 3D or N-D space according to 2, 3, or more sets x, y, etc.. of "template" coordinates sampled along each direction/dimension of the space that you want to mesh.
Hence, the matrix or hypermatrix X is made by replicating the vector x as all its columns ; the matrix or hypermatrix Y is made by replicating the vector y as all its rows ; Z is made of replicating the vector z along all its local thicknesses (3rd dimension); etc.
--> [X, Y] = ndgrid([1 3 4], [0 2 4 6]) X = 1. 1. 1. 1. 3. 3. 3. 3. 4. 4. 4. 4. Y = 0. 2. 4. 6. 0. 2. 4. 6. 0. 2. 4. 6.
Then, the coordinates of the node(i,j) in the 2D space will be simply [x(i), y(j)] now given by [X(i,j), Y(i,j)]. As well, the coordinates of a node(i,j,k) of a 3D grid will be [x(i), y(j), z(k)] now given by [X(i,j,k), Y(i,j,k), Z(i,j,k)].
This replication scheme can be generalized to any number of dimensions, as well to any type of uniform data. Let's for instance consider 2 attributes:
- The first is a number, to be chosen from the vector say
n= [ 3 7 ] - The second is a letter, to be chosen from the vector say
c= ["a" "e" "i" "o" "u" "y"]
--> [N, C] = ndgrid([3 7],["a" "e" "i" "o" "u" "y"]) C = !a e i o u y ! !a e i o u y ! N = 3. 3. 3. 3. 3. 3. 7. 7. 7. 7. 7. 7.
Then, the object(i,j) will have the properties {n(i) c(j)} that now can be addressed with {N(i,j) C(i,j)}. This kind of grid may be useful to initialize an array of structures.
Following examples show how to use X, Y, Z in most frequent applications.
Examples
Example #1:
// Create a simple 2d grid x = linspace(-10,2,40); y = linspace(-5,5,40); [X,Y] = ndgrid(x,y); // Compute ordinates Z(X,Y) on the {X, Y} grid and plot Z(X,Y) Z = X - 3*X.*sin(X).*cos(Y-4) ; clf() plot3d(x,y,Z, flag=[color("green") 2 4], alpha=7, theta=60); show_window()
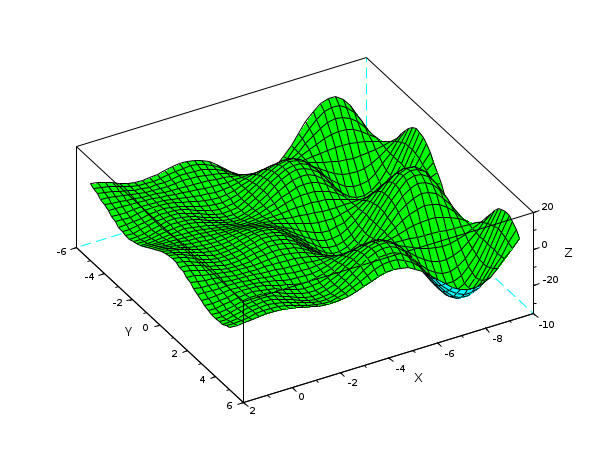
Example #2:
// Create a simple 3d grid nx = 10; ny = 6; nz = 4; x = linspace(0,2,nx); y = linspace(0,1,ny); z = linspace(0,0.5,nz); [X,Y,Z] = ndgrid(x,y,z); // Try to display this 3d grid XF=[]; YF=[]; ZF=[]; for k=1:nz [xf,yf,zf] = nf3d(X(:,:,k),Y(:,:,k),Z(:,:,k)); XF = [XF xf]; YF = [YF yf]; ZF = [ZF zf]; end for j=1:ny [xf,yf,zf] = nf3d(matrix(X(:,j,:),[nx,nz]),... matrix(Y(:,j,:),[nx,nz]),... matrix(Z(:,j,:),[nx,nz])); XF = [XF xf]; YF = [YF yf]; ZF = [ZF zf]; end clf() plot3d(XF,YF,ZF, flag=[0 6 3], 66, 61,leg="X@Y@Z") xtitle("A 3d grid !"); show_window()
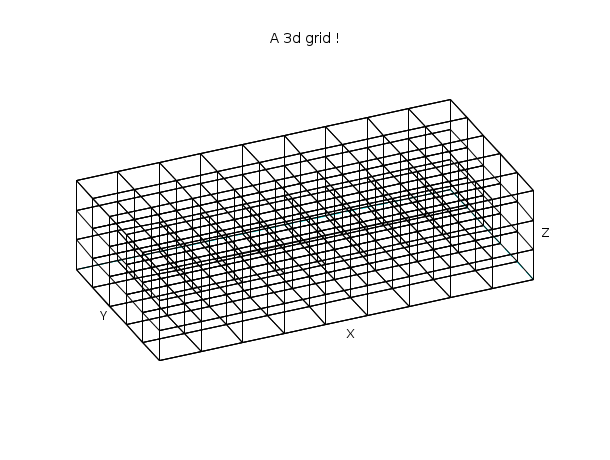
Example #3: Creates a table of digrams:
[c1, c2] = ndgrid(["a" "b" "c"], ["a" "b" "c" "d" "e" "f" "g" "h"]) c1+c2
--> [c1, c2] = ndgrid(["a" "b" "c"], ["a" "b" "c" "d" "e" "f" "g" "h"]) c2 = !a b c d e f g h ! !a b c d e f g h ! !a b c d e f g h ! c1 = !a a a a a a a a ! !b b b b b b b b ! !c c c c c c c c ! --> c1+c2 ans = !aa ab ac ad ae af ag ah ! !ba bb bc bd be bf bg bh ! !ca cb cc cd ce cf cg ch !
See also
History
| Version | Description |
| 6.0.0 | Extension to all homogeneous datatypes ([], booleans, encoded integers, polynomials, rationals, strings). Revision of the help page. |
| 6.0.1 | ndgrid(x) is now accepted: Default y=x. |
| Report an issue | ||
| << meshgrid | Matrix generation | ones >> |