remezb

Minimax approximation of magnitude response

Syntax

[an]=remezb(nc,fg,ds,wt)

Arguments

nc: Number of cosine functions
fg: Grid of frequency points in [0,.5)
ds: Desired magnitude on grid fg
wt: Weighting function on error on grid fg
an: Cosine filter coefficients

Description

Minimax approximation of a frequency domain magnitude response. The approximation takes the form h = sum[a(n)*cos(wn)] for n=0,1,...,nc. An FIR, linear-phase filter can be obtained from the output of the function by using the following commands

hn(1:nc-1)=an(nc:-1:2)/2;
hn(nc)=an(1);
hn(nc+1:2*nc-1)=an(2:nc)/2;

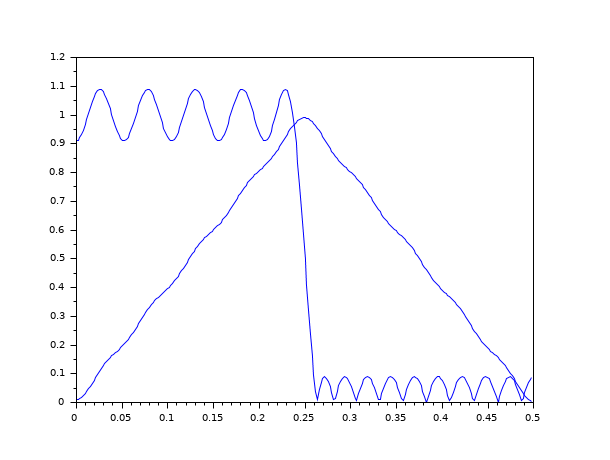
Examples

// Choose the number of cosine functions and create a dense grid
// in [0,.24) and [.26,.5)
nc=21;ngrid=nc*16;
fg=.24*(0:ngrid/2-1)/(ngrid/2-1);
fg(ngrid/2+1:ngrid)=fg(1:ngrid/2)+.26*ones(1:ngrid/2);

// Specify a low pass filter magnitude for the desired response
ds(1:ngrid/2)=ones(1:ngrid/2);
ds(ngrid/2+1:ngrid)=zeros(1:ngrid/2);

// Specify a uniform weighting function
wt=ones(fg);

// Run remezb
an=remezb(nc,fg,ds,wt)

// Make a linear phase FIR filter
hn(1:nc-1)=an(nc:-1:2)/2;
hn(nc)=an(1);
hn(nc+1:2*nc-1)=an(2:nc)/2;

// Plot the filter's magnitude response
plot(.5*(0:255)/256,frmag(hn,256));

// Choose the number of cosine functions and create a dense grid in [0,.5)
nc=21; ngrid=nc*16;
fg=.5*(0:(ngrid-1))/ngrid;

// Specify a triangular shaped magnitude for the desired response
ds(1:ngrid/2)=(0:ngrid/2-1)/(ngrid/2-1);
ds(ngrid/2+1:ngrid)=ds(ngrid/2:-1:1);

// Specify a uniform weighting function
wt=ones(fg);

// Run remezb
an=remezb(nc,fg,ds,wt)

// Make a linear phase FIR filter
hn(1:nc-1)=an(nc:-1:2)/2;
hn(nc)=an(1);
hn(nc+1:2*nc-1)=an(2:nc)/2;

// Plot the filter's magnitude response
plot(.5*(0:255)/256,frmag(hn,256));

Report an issue
<< remez	Filters	srfaur >>

remezb

Syntax

Arguments

Description

Examples

See also