arl2

Arguments

y

real vector or polynomial in z^-1, it contains the coefficients of the Fourier's series of the rational system to approximate (the impulse response)

den0

a polynomial which gives an initial guess of the solution, it may be poly(1,'z','c')

n

integer, the degree of approximating transfer function (degree of den)

imp

integer in (0,1,2) (verbose mode)

h

transfer function num/den or transfer matrix (column vector) when flag 'all' is given.

den

polynomial or vector of polynomials, contains the denominator(s) of the solution(s)

num

polynomial or vector of polynomials, contains the numerator(s) of the solution(s)

err

real constant or vector , the l2-error achieved for each solutions

Description

[den,num,err]=arl2(y,den0,n [,imp]) finds a pair of polynomials num and den such that the transfer function num/den is stable and its impulse response approximates (with a minimal l2 norm) the vector y assumed to be completed by an infinite number of zeros.

If y(z) = y(1)(1/z)+y(2)(1/z^2)+ ...+ y(ny)(1/z^ny)

then l2-norm of num/den - y(z) is err.

n is the degree of the polynomial den.

The num/den transfer function is a L2 approximant of the Fourier's series of the rational system.

Various intermediate results are printed according to imp.

[den,num,err]=arl2(y,den0,n [,imp],'all') returns in the vectors of polynomials num and den a set of local optimums for the problem. The solutions are sorted with increasing errors err. In this case den0 is already assumed to be poly(1,'z','c')

Examples

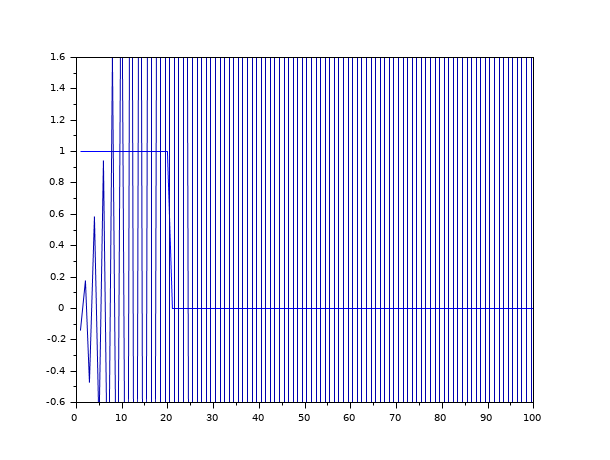
v = ones(1,20);
clf();
plot2d([], [v';zeros(80,1)], 2, '051',' ',[1,-0.5,100,1.5])

[d,n,e] = arl2(v, poly(1,'z','c'),1)
plot2d([], ldiv(n,d,100), 2, '000')
[d,n,e] = arl2(v,d,3)
plot2d([], ldiv(n,d,100), 3, '000')
[d,n,e] = arl2(v,d,8)
plot2d([], ldiv(n,d,100), 5, '000')

[d,n,e] = arl2(v,poly(1,'z','c'),4,'all')
plot2d([], ldiv(n(1),d(1),100), 10, '000')

See also

• ldiv — divisão longa entre matrizes de polinômios
• imrep2ss — state-space realization of an impulse response
• time_id — SISO least square identification
• armax — armax identification
• frep2tf — transfer function realization from frequency response