Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
fft
Transformée de Fourier discrète rapide.
ifft
Transformée de Fourier discrète rapide inverse.
Séquence d'appel
X=fft(A [,sign] [,option]) X=fft(A,sign,selection [,option]) X=fft(A,sign,dims,incr [,option] )
Arguments
- A
un tableau de nombres réels ou complexes (vecteur, matrice, ou tableau N-dimensionnel).
- X
un tableau de nombres réels ou complexes ayant les mêmes dimensions que
A.- sign
- un entier. qui peut prendre les valeurs
1ou-1. Détermine le sens de la transformation. La valeur par défaut est-1(transformée directe). - option
- une chaîne de caratères. qui peut prendre les valeurs
"symmetric"ou"nonsymmetric". Permet d'indiquer à l'algorithme siAest symmétrique ou non. Si cet argument est omis l'algorithme determine automatiquement siAest symmétrique ou non. Voir la partie "Description" pour plus de détails. - selection
- un vecteur contenant des index sur les dimensions de
A. Voir la partie "Description" pour plus de détails. - dims
un vecteur de nombres positifs à valeurs entières, ou un vecteur d'entiers positifs. Voir la partie "Description" pour plus de détails.
Chaque élément doit être un diviseur du nombre total d'éléments de
A.Le produit des éléments de
dimsdoit être strictement inférieur au nombre total d'éléments deA.- incr
un vecteur de nombres positifs à valeurs entières, ou un vecteur d'entiers positifs. Voir la partie "Description" pour plus de détails.
Le nombre d'éléments de
incrdoit être égal au nombre d'éléments dedims.Chaque élément doit être un diviseur du nombre total d'éléments de
A.Les éléments de
incrdoivent être en ordre strictement croissant.
Description
Cette fonction calcule la transformée de Fourier discrete directe ou inverse, mono ou multi dimensionnelle- Syntaxe courte
- direct
X=fft(A,-1 [,option])ouX=fft(A [,option])calcule la transformée de Fourier discrète directe deA- monovariable
Si
Aest un vecteurx=fft(a,-1)oux=fft(a)calcule une transformée monovariable, c'est à dire: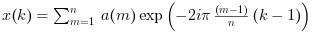
A noter: (l'argument
-1argument de la fonctionfftreprésente le signe de l'exposant de l'exponentielle.- multivariable
Si
Aest une matrice, ou un tableau multi-diemnsionnel,X=fft(A,-1)ouX=fft(A)calcule la transformée de Fourier discrète directe multivariable deA.
- inverse
X=fft(A,1)orX=ifft(A)calcule la transformée inverse normalisée, telle queA==ifft(fft(A)).- mono-variable
Si
Aest un vecteurX=fft(A,+1)ouX=ifft(A)calcule une transformée monovariable inverse, c'est à dire: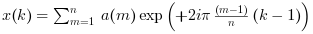
- multi variable
X=fft(A,+1)ouX=ifft(A)calcule la transformée de Fourier discrète inverse multivariable deA
- Syntaxe longue pour la FFT mutidimensionnelle
X=fft(A,sign,selection [,option])permet de calculer efficacement les transformées directes ou inverses de toutes les "tranches" deAcorrespondant à la selection de dimensions.Par exemple si,
Aest un tableau 3-D,X=fft(A,-1,2)est équivalent à:et
X=fft(A,-1,[1 3])est équivalent à:X=fft(A,sign,dims,incr [,option])est une syntaxe ancienne qui permet aussi de calculer efficacement les transformées directes ou inverses de toutes les "tranches" deALa sélection des "tranches" se faisant par la donnée des dimensions et des incréments associés à chacune des dimensions. Avec cette syntaxe les dimensions effectives deAne sont pas prises en compte.Par example si
Aest un tableau ayantn1*n2*n3élémentsX=fft(A,-1,n1,1)est équivalent àX=fft(matrix(A,[n1,n2,n3]),-1,1). etX=fft(A,-1,[n1 n3],[1 n1*n2])est équivalent àX=fft(matrix(A,[n1,n2,n3]),-1,[1,3]).
- utilisation de l'argument option Cet argument
peut être utilisé pour informer l'algorithme de fft au sujet
de la symétrie de
Aou de toutes ses "tranches". Un tableau multi-dimensionnelBqui a pour dimensionsn1, ...,npest symétrique conjugué pour la fft si et seulement siB==conj(B([1 n1:-1:2],[1 n2:-1:2],...,[1 np:-1:2])).Dans un tel cas le résultat de la fft est réel et un algorithme spécifique peut-être utilisé pour amélioer l'éfficacité et réduire le coût mémoire. - "symmetric" Cette valeur indique à
l'algorithme de considérer que
Aou toutes ses "tranches" est symétrique conjugué. Cette option est utile pour éviter le surcoùt de la détermination automatique de la symétrie et pour gérer les cas oùAn'est pas exactement symmétrique du fait par exemple d'erreurs d'arrondis. - "nonsymmetric" Cette valeur force l'algorithme à ne pas prendre en compte une éventuelle symétrie.
- non spécifié Si l'argument
optionest omis l'algorithme va réaliser automatiquement un test de symmétrie exacte.
- "symmetric" Cette valeur indique à
l'algorithme de considérer que
- Optimisation de l'efficacité de la fft
Remarque: la fonction
fftsauve automatiquement des paramêtres en mémoire (wisdom) pour accélérer les calculs de fft suivants correspondants aux mêmes dimensions et mêmes options.Les fonctions get_fftw_wisdom, set_fftw_wisdom permettent de récupérer et recharger ces paramètres pour amélioer l'efficacité de calcul de fft lorsque l'on alterne plusieurs types de fft.
Algorithmes
Cette fonction est basée sur la bibliothèque fftw3.
Examples
1-D fft
//Composantes fréquentielles d'un signal //---------------------------------- // Construction d'un signal bruité échantilloné à 1000hz // contenant deux fréquences pures à 50 et 70 Hz. sample_rate=1000; t = 0:1/sample_rate:0.6; N=size(t,'*'); //nombre d'échantillons s=sin(2*%pi*50*t)+sin(2*%pi*70*t+%pi/4)+grand(1,N,'nor',0,1); y=fft(s); //y est symétrique, on ne garde que N/2 points f=sample_rate*(0:(N/2))/N; //vecteur de fréquences associé n=size(f,'*') clf() plot(f,abs(y(1:n)))
2-D fft
//---------------------------------- A = zeros(256,256); A(5:24,13:17) = 1; X = fftshift(fft(A)); set(gcf(),"color_map",jetcolormap(128)); clf;grayplot(0:255,0:255,abs(X)')
mupliple fft
//simple case, 3 1-D fft at a time N=2048; t=linspace(0,10,2048); A=[2*sin(2*%pi*3*t)+ sin(2*%pi*3.5*t) 10*sin(2*%pi*8*t) sin(2*%pi*0.5*t)+4*sin(2*%pi*0.8*t)]; X=fft(A,-1,2); fs=1/(t(2)-t(1)); f=fs*(0:(N/2))/N; //associated frequency vector clf;plot(f(1:100)',abs(X(:,1:100))') legend(["3 and 3.5 Hz","8 Hz","0.5 and 0.8 Hz"],"in_upper_left") // 45 3-D fft at a time Dims=[5 4 9 5 6]; A=matrix(rand(1,prod(Dims)),Dims); y=fft(A,-1,[2 4 5]); //equivalent (but less efficient code) y1=zeros(A); for i1=1:Dims(1) for i3=1:Dims(3) ind=list(i1,:,i3,:,:); y1(ind(:))=fft(A(ind(:)),-1); end end
//Définition directe de la transformée de Fourier discrete //-------------------------------------------------------- function xf=DFT(x, flag); n=size(x,'*'); //Calcul de la matrice de Fourier (n by n !) if flag==1 then,//transformation inverse am=exp(2*%pi*%i*(0:n-1)'*(0:n-1)/n); else //transformation directe am=exp(-2*%pi*%i*(0:n-1)'*(0:n-1)/n); end xf=am*matrix(x,n,1);//dft xf=matrix(xf,size(x));//mise en formz if flag==1 then,xf=xf/n;end endfunction //Comparaison avec l'algorithme de la transformée rapide: a=rand(1,1000); norm(DFT(a,1) - fft(a,1)) norm(DFT(a,-1) - fft(a,-1)) timer();DFT(a,-1);timer() timer();fft(a,-1);timer()
Voir aussi
- corr — correlation, covariance
- fftw_flags — choix de la méthode pour la sélection de l'algorithme de planification pour la fft
- get_fftw_wisdom — retourne le wisdom fftw
- set_fftw_wisdom — charge un wisdom fftw
- fftw_forget_wisdom — Réinitialise le wisdom fftw
Bibliographie
Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation
| Report an issue | ||
| << dst | Tranformées | fft2 >> |