factorial

factorial function : product of the n first positive integers

Syntax

f = factorial(n)
[f, p] = factorial(n)
[f, p, m] = factorial(n)

Arguments

n: scalar, vector, matrix or hypermatrix of positive integers <= 10¹⁴.
f: array of doubles, of the sizes of n: f(i) = n(i)!. f values are exact up to n=21 included.
p: array of doubles, of the sizes of n: power of 10 of f: p(i) = int(log10(f(i)!)).
m: array of doubles in [1,10[, of the sizes of n: Mantissae of f, such that n(i)! = m(i) * 10^p(i).

Description

Returns the factorial of n, that is the product 1 * 2 * ... * n.

f overflows as soon as n>170 and always returns %inf for any bigger n.

For n in [22, 170], the relative accuracy of f is roughly %eps ~ 2e-16.
For n in [171, 1.0x10¹⁴], the power p value is exact, and the relative accuracy of the mantissa m goes roughly as n*%eps ~ n * 1e-16 (see the last example).
Beyond n > 10.0¹⁴, p becomes > 1/%eps and gets truncated. It is then no longer possible to retrieve a reliable mantissa.

Graph

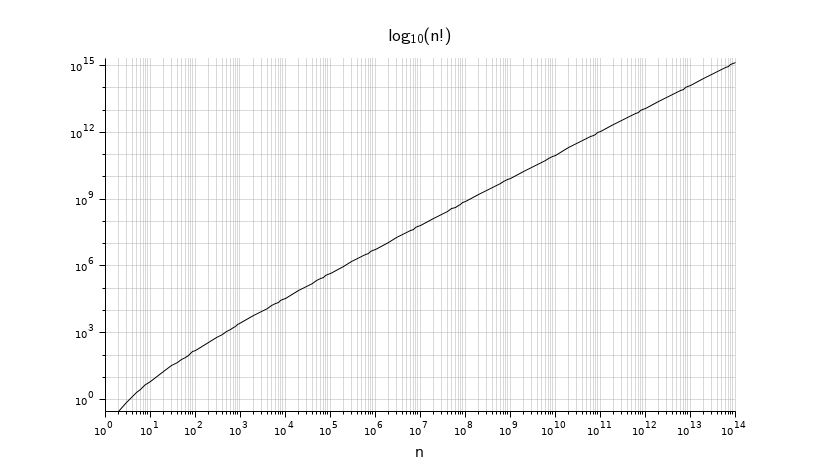
Examples

Table of the first n! exact values :

format(22);
n = (0:21)';
[n factorial(n)]
format(10);

--> [n factorial(n)]
 ans  =
   0.    1.
   1.    1.
   2.    2.
   3.    6.
   4.    24.
   5.    120.
   6.    720.
   7.    5040.
   8.    40320.
   9.    362880.
   10.   3628800.
   11.   39916800.
   12.   479001600.
   13.   6227020800.
   14.   87178291200.
   15.   1307674368000.
   16.   20922789888000.
   17.   355687428096000.
   18.   6402373705728000.
   19.   121645100408832000.
   20.   2432902008176640000.
   21.   51090942171709440000.

Ceiling of factorial() in floating point representation:

factorial(170) // 7.257415615307998967e306
factorial(171) // %inf

Plot the function on its whole range:

x = (10^(0:13)).*.(1:9); x(1)=[]; x($)=1e14;
[f, p, m] = factorial(x);
clf
plot2d("ll", x, p+log10(m))
xlabel("n", "fontsize",3)
title("$\mathsf{log_{10}(n!)}$", "fontsize", 4)
xgrid(color("grey70"), 1, 7)
set(gca(), "sub_ticks",[8 2], "tight_limits","on");
gca().data_bounds([1 4]) = [1 2e15];
gcf().axes_size = [850 480];

Relative factorial() errors:

n = 10^(1:14)';
[f, p, m] = factorial(n);
// Exact (truncated) mantissae for n = 10^(1:14) :
m0 = [
   3.6288000000000000  9.3326215443944153  4.0238726007709377 ..  // n = 10     100   1000
   2.8462596809170545  2.8242294079603479                     ..  // n = 10000  100000
   8.2639316883312401  1.2024233400515904  1.6172037949214624 ..  // n = 1e6    1e7   1e8
   9.9046265792229937  2.3257962056730834  3.7489285991050270 ..  // n = 1e9    1e10  1e11
   1.4036611603737561  2.4033300843401153  1.6456020559872979     // n = 1e12   1e13  1e14
   ]';
r_err = m./m0 - 1;
[n r_err]

--> [n r_err]
 ans  =
   10.          0.
   100.        -5.551D-16
   1000.        1.132D-13
   10000.       1.918D-12
   100000.      6.611D-12
   1000000.     9.962D-11
   10000000.    5.048D-08
   100000000.   1.050D-08
   1.000D+09   0.0000001
   1.000D+10   0.0000019
   1.000D+11   0.0000062
   1.000D+12   0.0001327
   1.000D+13   0.0004839
   1.000D+14   0.0071116

History

Version	Description
6.1	Extension up to n = 10¹⁴. `p` 10-power and `m` mantissa output added.

Report an issue
<< factor	Discrete mathematics	gcd >>

Copyright (c) 2022-2024 (Dassault Systèmes)
Copyright (c) 2017-2022 (ESI Group)
Copyright (c) 2011-2017 (Scilab Enterprises)
Copyright (c) 1989-2012 (INRIA)
Copyright (c) 1989-2007 (ENPC)
with contributors

Last updated:
Tue Feb 25 08:49:18 CET 2020