leastsq

Arguments

fopt

value of the function f(x)=||fun(x)||^2 at xopt

xopt

best value of x found to minimize ||fun(x)||^2

gopt

gradient of f at xopt

fun

a scilab function or a list defining a function from R^n to R^m (see more details in DESCRIPTION).

x0

real vector (initial guess of the variable to be minimized).

dfun

a scilab function or a string defining the Jacobian matrix of fun (see more details in DESCRIPTION).

cstr

bound constraints on x. They must be introduced by the string keyword 'b' followed by the lower bound binf then by the upper bound bsup (so cstr appears as 'b',binf,bsup in the syntax). Those bounds are real vectors with same dimension than x0 (-%inf and +%inf may be used for dimension which are unrestricted).

algo

a string with possible values: 'qn' or 'gc' or 'nd'. These strings stand for quasi-Newton (default), conjugate gradient or non-differentiable respectively. Note that 'nd' does not accept bounds on x.

iprint

scalar argument used to set the trace mode. iprint=0 nothing (except errors) is reported, iprint=1 initial and final reports, iprint=2 adds a report per iteration, iprint>2 add reports on linear search. Warning, most of these reports are written on the Scilab standard output.

df0

real scalar. Guessed decreasing of ||fun||^2 at first iteration. (df0=1 is the default value).

mem

integer, number of variables used to approximate the Hessian (second derivatives) of f when algo='qn'. Default value is 10.

stop

sequence of optional parameters controlling the convergence of the algorithm. They are introduced by the keyword 'ar', the sequence being of the form 'ar',nap, [iter [,epsg [,epsf [,epsx]]]]

nap

maximum number of calls to fun allowed.

iter

maximum number of iterations allowed.

epsg

threshold on gradient norm.

epsf

threshold controlling decreasing of f

epsx

threshold controlling variation of x. This vector (possibly matrix) of same size as x0 can be used to scale x.

Description

The leastsq function solves the problem

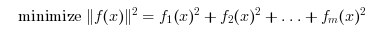
where f is a function from R^n to R^m. Bound constraints cab be imposed on x.

How to provide fun and dfun

fun can be a scilab function (case 1) or a fortran or a C routine linked to scilab (case 2).

case 1:

When fun is a Scilab function, its calling sequence must be:

y=fun(x)
 

In the case where the cost function needs extra parameters, its header must be:

y=f(x,a1,a2,...)
 

In this case, we provide fun as a list, which contains list(f,a1,a2,...).

case 2:

When fun is a Fortran or C routine, it must be list(fun_name,m[,a1,a2,...]) in the syntax of leastsq, where fun_name is a 1-by-1 matrix of strings, the name of the routine which must be linked to Scilab (see link). The header must be, in Fortran:

subroutine fun(m, n, x, params, y)
integer m,n
double precision x(n), params(*), y(m)
 

and in C:

void fun(int *m, int *n, double *x, double *params, double *y)
 

where n is the dimension of vector x, m the dimension of vector y, with y=fun(x), and params is a vector which contains the optional parameters a1, a2, .... Each parameter may be a vector, for instance if a1 has 3 components, the description of a2 begin from params(4) (in fortran), and from params[3] (in C). Note that even if fun does not need supplementary parameters you must anyway write the fortran code with a params argument (which is then unused in the subroutine core).

By default, the algorithm uses a finite difference approximation of the Jacobian matrix. The Jacobian matrix can be provided by defining the function dfun, where to the optimizer it may be given as a usual scilab function or as a fortran or a C routine linked to scilab.

case 1:

when dfun is a scilab function, its calling sequence must be:

              y=dfun(x)
 

where y(i,j)=dfi/dxj. If extra parameters are required by fun, i.e. if arguments a1,a2,... are required, they are passed also to dfun, which must have header

              y=dfun(x,a1,a2,...)
 

Note that, even if dfun needs extra parameters, it must appear simply as dfun in the syntax of leastsq.

case 2:

When dfun is defined by a Fortran or C routine it must be a string, the name of the function linked to Scilab. The calling sequences must be, in Fortran:

subroutine dfun(m, n, x, params, y)
integer m,n
double precision x(n), params(*), y(m,n)
 

in C:

          void fun(int *m, int *n, double *x, double *params, double *y)
 

In the C case y(i,j)=dfi/dxj must be stored in y[m*(j-1)+i-1].

Remarks

Like datafit, leastsq is a front end onto the optim function. If you want to try the Levenberg-Marquard method instead, use lsqrsolve.

A least squares problem may be solved directly with the optim function ; in this case the function NDcost may be useful to compute the derivatives (see the NDcost help page which provides a simple example for parameters identification of a differential equation).

Examples

We will show different calling possibilities of leastsq on one (trivial) example which is non linear but does not really need to be solved with leastsq (applying log linearizes the model and the problem may be solved with linear algebra). In this example we look for the 2 parameters x(1) and x(2) of a simple exponential decay model (x(1) being the unknown initial value and x(2) the decay constant):

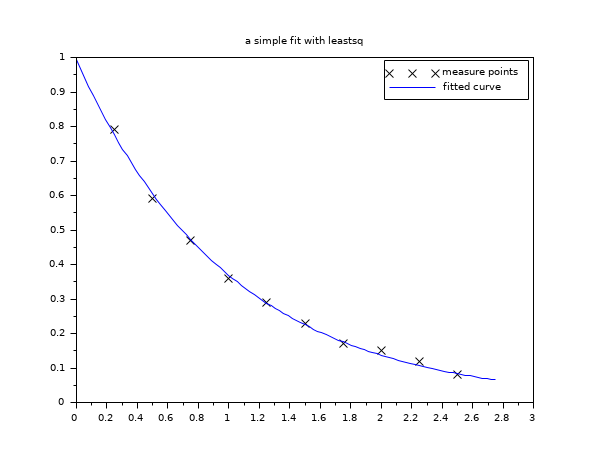
function y=yth(t, x)
   y  = x(1)*exp(-x(2)*t)
endfunction

// we have the m measures (ti, yi):
m = 10;
tm = [0.25, 0.5, 0.75, 1.0, 1.25, 1.5, 1.75, 2.0, 2.25, 2.5]';
ym = [0.79, 0.59, 0.47, 0.36, 0.29, 0.23, 0.17, 0.15, 0.12, 0.08]';
// measure weights (here all equal to 1...)
wm = ones(m,1);

// and we want to find the parameters x such that the model fits the given
// data in the least square sense:
//
//  minimize  f(x) = sum_i  wm(i)^2 ( yth(tm(i),x) - ym(i) )^2

// initial parameters guess
x0 = [1.5 ; 0.8];

// in the first examples, we define the function fun and dfun
// in scilab language
function e=myfun(x, tm, ym, wm)
   e = wm.*( yth(tm, x) - ym )
endfunction

function g=mydfun(x, tm, ym, wm)
   v = wm.*exp(-x(2)*tm)
   g = [v , -x(1)*tm.*v]
endfunction

// now we could call leastsq:

// 1- the simplest call
[f,xopt, gopt] = leastsq(list(myfun,tm,ym,wm),x0)

// 2- we provide the Jacobian
[f,xopt, gopt] = leastsq(list(myfun,tm,ym,wm),mydfun,x0)

// a small graphic (before showing other calling features)
tt = linspace(0,1.1*max(tm),100)';
yy = yth(tt, xopt);
scf();
plot(tm, ym, "kx")
plot(tt, yy, "b-")
legend(["measure points", "fitted curve"]);
xtitle("a simple fit with leastsq")

// 3- how to get some information (we use iprint=1)
[f,xopt, gopt] = leastsq(1,list(myfun,tm,ym,wm),mydfun,x0)

// 4- using the conjugate gradient (instead of quasi Newton)
[f,xopt, gopt] = leastsq(1,list(myfun,tm,ym,wm),mydfun,x0,"gc")

// 5- how to provide bound constraints (not useful here !)
xinf = [-%inf,-%inf];
xsup = [%inf, %inf];
// without Jacobian:
[f,xopt, gopt] = leastsq(list(myfun,tm,ym,wm),"b",xinf,xsup,x0)
// with Jacobian :
[f,xopt, gopt] = leastsq(list(myfun,tm,ym,wm),mydfun,"b",xinf,xsup,x0)

// 6- playing with some stopping parameters of the algorithm
//    (allows only 40 function calls, 8 iterations and set epsg=0.01, epsf=0.1)
[f,xopt, gopt] = leastsq(1,list(myfun,tm,ym,wm),mydfun,x0,"ar",40,8,0.01,0.1)

Examples with compiled functions

Now we want to define fun and dfun in Fortran, then in C. Note that the "compile and link to scilab" method used here is believed to be OS independent (but there are some requirements, in particular you need a C and a fortran compiler, and they must be compatible with the ones used to build your scilab binary).

Let us begin by an example with fun and dfun in fortran

// 7-1/ Let 's Scilab write the fortran code (in the TMPDIR directory):
f_code = ["      subroutine myfun(m,n,x,param,f)"
          "*     param(i) = tm(i), param(m+i) = ym(i), param(2m+i) = wm(i)"
          "      implicit none"
          "      integer n,m"
          "      double precision x(n), param(*), f(m)"
          "      integer i"
          "      do i = 1,m"
          "         f(i) = param(2*m+i)*( x(1)*exp(-x(2)*param(i)) - param(m+i) )"
          "      enddo"
          "      end ! subroutine fun"
          ""
          "      subroutine mydfun(m,n,x,param,df)"
          "*     param(i) = tm(i), param(m+i) = ym(i), param(2m+i) = wm(i)"
          "      implicit none"
          "      integer n,m"
          "      double precision x(n), param(*), df(m,n)"
          "      integer i"
          "      do i = 1,m"
          "         df(i,1) =  param(2*m+i)*exp(-x(2)*param(i))"
          "         df(i,2) = -x(1)*param(i)*df(i,1)"
          "      enddo"
          "      end ! subroutine dfun"];
cd TMPDIR;
mputl(f_code,TMPDIR+'/myfun.f')

// 7-2/ compiles it. You need a fortran compiler !
names = ["myfun" "mydfun"]
flibname = ilib_for_link(names,"myfun.f",[],"f");

// 7-3/ link it to scilab (see link help page)
link(flibname,names,"f")

// 7-4/ ready for the leastsq call: be carreful do not forget to
//      give the dimension m after the routine name !
[f,xopt, gopt] = leastsq(list("myfun",m,tm,ym,wm),x0)  // without Jacobian
[f,xopt, gopt] = leastsq(list("myfun",m,tm,ym,wm),"mydfun",x0) // with Jacobian

Last example: fun and dfun in C.

// 8-1/ Let 's Scilab write the C code (in the TMPDIR directory):
c_code = ["#include <math.h>"
          "void myfunc(int *m,int *n, double *x, double *param, double *f)"
          "{"
          "  /*  param[i] = tm[i], param[m+i] = ym[i], param[2m+i] = wm[i] */"
          "  int i;"
          "  for ( i = 0 ; i < *m ; i++ )"
          "    f[i] = param[2*(*m)+i]*( x[0]*exp(-x[1]*param[i]) - param[(*m)+i] );"
          "  return;"
          "}"
          ""
          "void mydfunc(int *m,int *n, double *x, double *param, double *df)"
          "{"
          "  /*  param[i] = tm[i], param[m+i] = ym[i], param[2m+i] = wm[i] */"
          "  int i;"
          "  for ( i = 0 ; i < *m ; i++ )"
          "    {"
          "      df[i] = param[2*(*m)+i]*exp(-x[1]*param[i]);"
          "      df[i+(*m)] = -x[0]*param[i]*df[i];"
          "    }"
          "  return;"
          "}"];

mputl(c_code,TMPDIR+'/myfunc.c')

// 8-2/ compiles it. You need a C compiler !
names = ["myfunc" "mydfunc"]
clibname = ilib_for_link(names,"myfunc.c",[],"c");

// 8-3/ link it to scilab (see link help page)
link(clibname,names,"c")

// 8-4/ ready for the leastsq call
[f,xopt, gopt] = leastsq(list("myfunc",m,tm,ym,wm),"mydfunc",x0)

See also

• lsqrsolve — minimize the sum of the squares of nonlinear functions, levenberg-marquardt algorithm
• optim — non-linear optimization routine
• NDcost — generic external for optim computing gradient using finite differences
• datafit — Parameter identification based on measured data
• external — objeto Scilab, função ou rotina externa
• qpsolve — linear quadratic programming solver