Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
calfrq
frequency response discretization
Syntax
[frq,bnds,split]=calfrq(h,fmin,fmax)
Arguments
- h
A siso or simo linear dynamical system, in state space, transfer function or zpk representations, in continuous or discrete time.
- fmin,fmax
real scalars (min and max frequencies in Hz)
- frq
row vector (discretization of the frequency interval)
- bnds
vector
[Rmin Rmax Imin Imax]whereRminandRmaxare the lower and upper bounds of the frequency response real part,IminandImaxare the lower and upper bounds of the frequency response imaginary part,- split
vector of frq splitting points indexes
Description
frequency response discretization; frq is the
discretization of [fmin,fmax] such that the peaks in
the frequency response are well represented.
Singularities are located between frq(split(k)-1)
and frq(split(k)) for k>1.
Examples
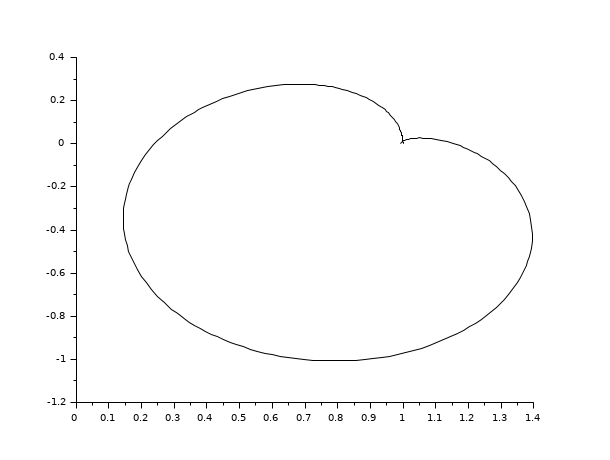
s=poly(0,'s') h=syslin('c',(s^2+2*0.9*10*s+100)/(s^2+2*0.3*10.1*s+102.01)) h1=h*syslin('c',(s^2+2*0.1*15.1*s+228.01)/(s^2+2*0.9*15*s+225)) [f1,bnds,spl]=calfrq(h1,0.01,1000); rf=repfreq(h1,f1); plot2d(real(rf)',imag(rf)')
See also
History
| Versão | Descrição |
| 6.0 | handling zpk representation |
| Report an issue | ||
| << bode_asymp | Frequency Domain | dbphi >> |