Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
xcov
離散自己/相互共分散を計算する
呼び出し手順
[c, lagindex] = xcov(x) [c, lagindex] = xcov(x, y) [c, lagindex] = xcov(.., maxlags) [c, lagindex] = xcov(.., maxlags, scaling)
パラメータ
- x
実数または複素浮動小数点数のベクトル.
- y
実数または複素浮動小数点数のベクトル. デフォルト値は
x.- maxlags
スカラーで1より大きな整数値.デフォルト値は
n. ただし,nはx,yベクトルの長さの大きい方です.- scaling
文字列で,値は以下のどれか:
"biased","unbiased","coeff","none". デフォルト値は"none".- c
実数または浮動小数点数のベクトルで,向きは
xと同じです.- lagindex
行ベクトルで,
cの値に 対応する添字(lag index)を有します.
説明
c=xcov(x)は,以下の正規化しない離散共分散を計算します:
そして,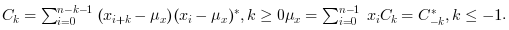
cを返します. 共分散の並びは, Ck=-n:n となります. ただし,nはxの長さです.xcov(x,y)は,以下のように正規化しない離散相互共分散を計算します:
結果を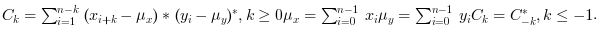
cに返します. 相互共分散の並びは, Ck=-n:n となります.ただし,nはxおよびyの長さの大きい方です.
maxlags 引数が指定された場合,
xcov は c を
返し,共分散の並びは Ck=-maxlags:maxlags と
なります.
maxlags が length(x)よりも
大きい場合, cの先頭と末尾の複数の値は
ゼロになります.
scaling 引数は,
cに結果を出力する前に
C(k)を正規化する方法を以下のように指定します:
- "biased":
c=C/n. - "unbiased":
c=C./(n-(-maxlags:maxlags)). - "coeff":
c=C/(norm(x)*norm(y)).
手法
この関数は,xcorr(x-mean(x),y-mean(y),...)により
Cを計算します.例
t = linspace(0, 100, 2000); y = 0.8 * sin(t) + 0.8 * sin(2 * t); [c, ind] = xcov(y, "biased"); plot(ind, c)
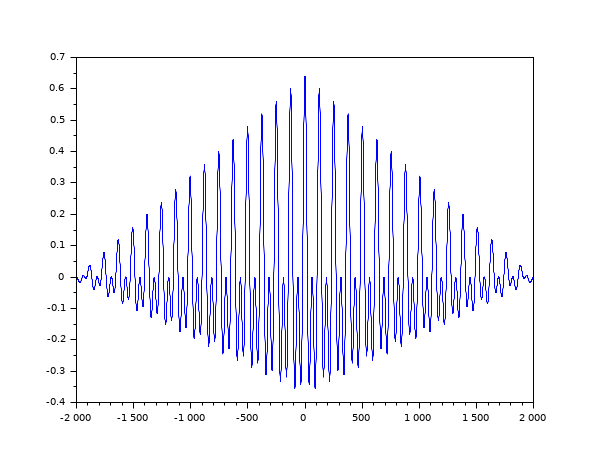
履歴
| バージョン | 記述 |
| 5.4.0 | xcov 追加. |
| Report an issue | ||
| << sincd | Signal Processing | FFTW >> |