Scilab 6.0.1
- Ajuda do Scilab
- Funções Elementares
- Trigonometria
- acos
- acosd
- acosh
- acoshm
- acosm
- acot
- acotd
- acoth
- acsc
- acscd
- acsch
- asec
- asecd
- asech
- asin
- asind
- asinh
- asinhm
- asinm
- atan
- atand
- atanh
- atanhm
- atanm
- cos
- cosd
- cosh
- coshm
- cosm
- cotd
- cotg
- coth
- cothm
- csc
- cscd
- csch
- csgn
- sec
- secd
- sech
- sin
- sinc
- sind
- sinh
- sinhm
- sinm
- tan
- tand
- tanh
- tanhm
- tanm
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
acosh
hyperbolic cosine inverse
Syntax
t = acosh(x)
Arguments
- x, t
each is a real or complex vector or matrix.
thas the sizes ofx.
Description
acosh(x) returns t such that
cosh(t)==x and real(t)>=0.
-t are always other possible answers.
For real input numbers -1 < x < 1,
real(t)==0 and imag(t)
belongs to ]0, %pi[.
For complex numbers x,
imag(t) belongs to [-pi, pi]
and any t + k*%pi*%i with integer k are other
possible answers.
Sample
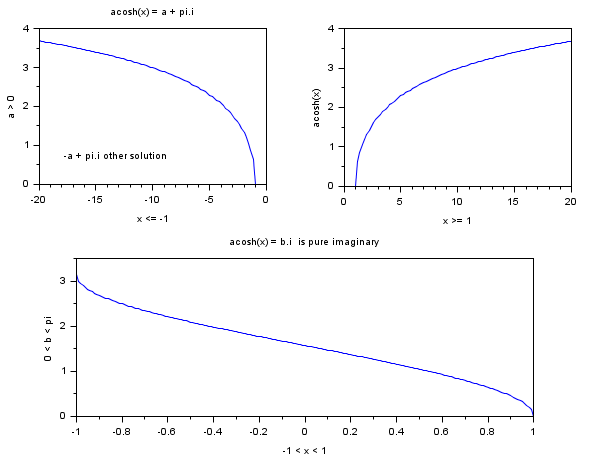
Examples
| Report an issue | ||
| << acosd | Trigonometria | acoshm >> |