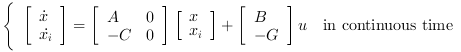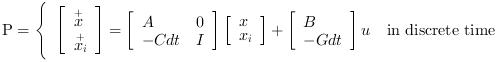Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
lqi
Linear quadratic integral compensator (full state)
Syntax
[K,X]=lqi(P,Q,R [,S])
Arguments
- P
The plant state space representation (see syslin) with nx states, nu inputs and ny outputs.
- Q
Real nx+ny by nx+ny symmetric matrix,
- R
full rank nu by nu real symmetric matrix
- S
real nx+ny by nu matrix, the default value is zeros(nx+ny,nu)
- K
a real matrix, the optimal gain
- X
a real symmetric matrix, the stabilizing solution of the Riccati equation
Description
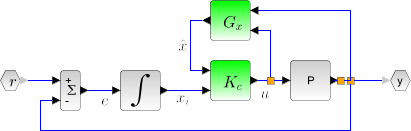
This function computes the linear quadratic integral full-state gain K for the plant P. The associated system block diagram is:
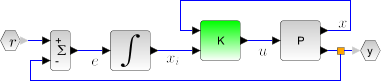
The plant P is given by its state space representation
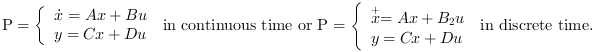
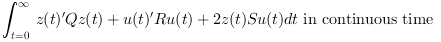
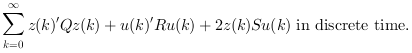
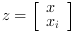 and
and 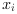 is the integrator(s) state(s);
is the integrator(s) state(s);Caution
It is assumed that matrix 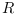 is non singular.
is non singular.
Remark
If the full state of the system is not available, An estimator of the plant state can be built using the lqe function.
Examples
Linear quadratic integral controller of a simplified disk drive using state observer.
//Disk drive model G=syslin("c",[0,32;-31.25,-0.4],[0;2.236068],[0.0698771,0]); t=linspace(0,20,2000); y=csim("step",t,G); //State estimator Wy=1; Wu=1; S=0; Q=G.B*Wu*G.B'; R=Wy+G.D*S + S'*G.D+G.D*Wu*G.D'; S=G.B*Wu*G.D'+S; //State estimator [Kf,X]=lqe(G,Q,R,S); Gx=observer(G,Kf); //LQI compensator wy=100; Q= wy*sysdiag(G.C'*G.C,1); R=1/wy; Kc=lqi(G,Q,R); //full controller K=lft([1;1]*(-Kc(1:2)*Gx(:,[2 1])+Kc(3)*[1/%s 0]),1);//e-->u //Full system H=(-K*G)/.(1);// full system transfer function y=csim("step",t,H); clf;plot(t,y)
See Also
| Report an issue | ||
| << lqg_ltr | Linéaire Quadratique | lqr >> |