Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
pspect
two sided cross-spectral estimate between 2 discrete time signals using the Welch's average periodogram method.
Syntax
[sm [,cwp]]=pspect(sec_step,sec_leng,wtype,x [,y] [,wpar]) [sm [,cwp]]=pspect(sec_step,sec_leng,wtype,nx [,ny] [,wpar])
Arguments
- x
vector, the time-domain samples of the first signal.
- y
vector, the time-domain samples of the second signal. If
yis omitted it is supposed to be equal tox(auto-correlation). If it is present, it must have the same numer of element thanx.- nx
a scalar : the number of samples in the
xsignal. In this case the segments of thexsignal are loaded by a user defined function namedgetx(see below).- ny
a scalar : the number of samples in the
ysignal. In this case the segments of the y signal are loaded by a user defined function namedgety(see below). If presentnymust be equal tonx.- sec_step
offset of each data window. The overlap
Dis given by sec_leng -sec_step. if sec_step==sec_leng/250% overlap is made. The overlap- sec_leng
Number of points of the window.
- wtype
The window type
're': rectangular'tr': triangular'hm': Hamming'hn': Hann'kr': Kaiser,in this case the wpar argument must be given'ch': Chebyshev, in this case the wpar argument must be given
- wpar
optional parameters for
Kaiser and Chebyshev windows:'kr':
wpar must be a strictly positive number'ch':
wparmust be a 2 element vector[main_lobe_width,side_lobe_height]with0<main_lobe_width<.5, andside_lobe_height>0
- sm
Two sided power spectral estimate in the interval
[0,1]of the normalized frequencies. It is a row array withsec_lenelements . The array is real in case of auto-correlation and complex in case of cross-correlation.The associated normalized frequencies array is
linspace(0,1,sec_len).- cwp
unspecified Chebyshev window parameter in case of Chebyshev windowing, or an empty matrix.
Description
Computes the cross-spectrum estimate of two signals
x and y if both are given and the
auto-spectral estimate of x otherwise. Spectral
estimate obtained using the modified periodogram method.
The cross spectrum of two signal x and y is defined to be
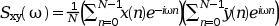
The modified periodogram method of spectral estimation repeatedly
calculates the periodogram of windowed sub-sections of the data contained
in x and y . These periodograms are
then averaged together and normalized by an appropriate constant to obtain
the final spectral estimate. It is the averaging process which reduces the
variance in the estimate.
For batch processing, the x and
y data may be read segment by segment using the
getxand gety user defined
functions. These functions have the following syntax:
xk=getx(ns,offset) and
yk=gety(ns,offset) where ns is the
segment size and offset is the index of the first
element of the segment in the full signal.
Reference
Oppenheim, A.V., and R.W. Schafer. Discrete-Time Signal Processing, Upper Saddle River, NJ: Prentice-Hall, 1999
Examples
rand('normal');rand('seed',0); x=rand(1:1024-33+1); //make low-pass filter with eqfir nf=33;bedge=[0 .1;.125 .5];des=[1 0];wate=[1 1]; h=eqfir(nf,bedge,des,wate); //filter white data to obtain colored data h1=[h 0*ones(1:max(size(x))-1)]; x1=[x 0*ones(1:max(size(h))-1)]; hf=fft(h1,-1); xf=fft(x1,-1);y=real(fft(hf.*xf,1)); //plot magnitude of filter h2=[h 0*ones(1:968)];hf2=fft(h2,-1);hf2=real(hf2.*conj(hf2)); hsize=max(size(hf2));fr=(1:hsize)/hsize;plot(fr,log(hf2)); //pspect example sm=pspect(100,200,'tr',y);smsize=max(size(sm));fr=(1:smsize)/smsize; plot(fr,log(sm)); rand('unif');
See also
- cspect — two sided cross-spectral estimate between 2 discrete time signals using the correlation method
- pspect — two sided cross-spectral estimate between 2 discrete time signals using the Welch's average periodogram method.
- mese — maximum entropy spectral estimation
- window — compute symmetric window of various type
| Report an issue | ||
| << mese | Spectral estimation | Transforms >> |