replot

引数

area

行ベクトル [xmin ymin xmax ymax] または [xmin ymin zmin xmax ymax zmax]: 再プロットされる領域の新しい範囲.

範囲を変えない場合は %nan を使用してください. %inf can be used to set a bound to the position of the most marginal graphical component existing in the axes, for the considered direction.

The default area is [%inf %inf %inf %inf] for a 2D axes, or [%inf %inf %inf %inf %inf %inf] for a 3D one.

If N axes are identified in idAxes, area may be a matrix with N rows and 4 or 6 columns. The row #i is then related to the axes #i of idAxes. If area is only a vector of 4 or 6 bounds, these ones are used for all axes to be reframed.

idAxes

Vector of graphic handles, expected to be of Axes type or to have direct children of type Axes, such as Figures and possibly frame uicontrols. idAxes specifies direct or children Axes to crop. If no axes is found, nothing is done.

By default, the current Axes is considered.

tight_limits

Single word "tight" or "on" or "off", or vector of 2 (in 2D) or 3 (in 3D) words "tight" or "on" or "off". If a single word is provided, it is used for every axis. This option forces the .tight_limits attribute of considered axes to the specified "on" or "off" values. By default, current limits modes are unchanged.

By default, current limits modes are unchanged.

説明

replot is used to reframe the (set of) axes specified with idAxes -- or by default the current axes -- with new boundaries defined by area = [xmin,ymin, xmax,ymax] or area = [xmin,ymin,zmin, xmax,ymax,zmax].

It changes the data_bounds attribute of processed axes.

When a specified bound is infinite (%inf and -%inf are equivalent), replot looks for the most marginal graphical object and sets the actual related bound to its position, taking also objects sizes into account. This ensures not clipping any object that would be beyond the targeted side of the axes.

When the tight_limits option is provided, its value is assigned to the .tight_limits attribute of each considered axes, in an axis-wise way.

例

// 最初の例
x=[0:0.1:2*%pi]';
plot2d(x,sin(x))
replot([-1,-1,10,2])

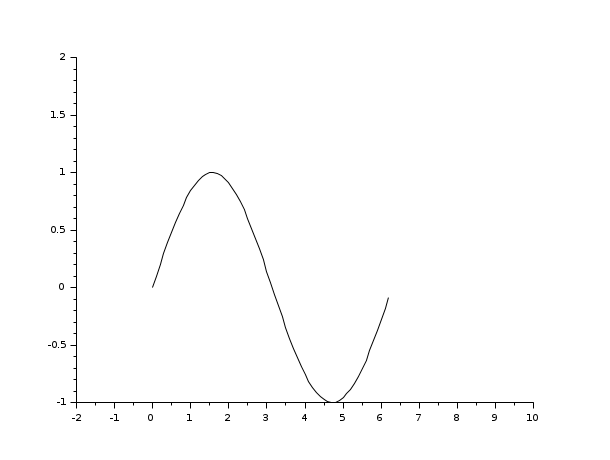
// 二番目の例
xdel(winsid());
plot() // plot demo
f=gcf();
replot([-1,-1,10,2],f.children(1)) // axesハンドルの値を指定
replot([-3,-2,8,4],f.children(2))

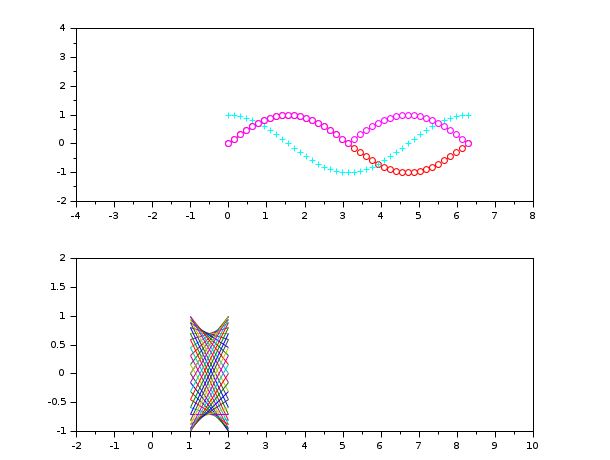
//値は%nanで示さ端子は変更されません。
x = linspace(0,360,200).';
clf
plot2d(x,[sind(x) tand(x)])
ax = gca();
ax.data_bounds              // 初期限界
replot([%nan,-10,%nan,10])  // YminとYmaxのだけ変更され
ax.data_bounds              // 新しい制限

// 3D端末Zも変更できます。
clf
x = linspace(-4,4,100);
X = meshgrid(x);
R = (X-0.5).^2 + (X.'+0.7).^2;
Z = sinc(R);
surf(x-0.5,x+0.7,Z)
f = gcf();
f.color_map = autumncolormap(100);
ax = gca();
ax.data_bounds
sleep(3000)
replot([-5 0 -0.4 0 5 0.5])
ax.data_bounds

// いくつかのグラフィカルなマーカーを同時にトリミングすることができます。
clf
x = linspace(-%pi,%pi,400);
subplot(2,2,1)
plot2d(x,sin(1 ./sqrt(abs(x))))
ax1 = gca();
subplot(2,2,2)
plot2d(x,sinh(sqrt(abs(x))))
subplot(2,1,2)
plot2d(x,cos(1 ./sqrt(abs(x))))
ax2 = gca();
sleep(4000)
f = gcf();
replot([-1 %nan 1.5 %nan], [ax1 ax2])

参照

• zoom_rect — カレントのグラフィック図の選択した部分をズーム
• rubberbox — 矩形選択用の輪ゴムボックス
• axes_properties — axesエンティティプロパティの説明

履歴