Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
However, this page did not exist in the previous stable version.
How to design an elliptic filter
楕円フィルタの設計法 (アナログおよびデジタル)
説明
このヘルプの目的は,アナログおよびデジタル楕円フィルタを簡単に設計することです.
アナログ楕円フィルタを設計する
楕円ローパスフィルタを設計する複数の手法があります. analpf または zpellを使用することができます. フィルタの極およびゼロを得る際にzpellを使用します. これらの極及びゼロを取得した後,この形式をsyslin の形式に変換する必要があります.
次に,フィルタはボード線図に表すことができます.
// analog elliptic (Bessel), order 2, cutoff 1 Hz Epsilon = 3; // 通過域のフィルタのリップル (0<epsilon<1) A = 60; // 阻止域のフィルタの減衰 (A<1) OmegaC = 10; // 通過域カットオフ周波数 (Hz) OmegaR = 50; // 阻止域カットオフ周波数 (Hz) // フィルタを生成 [_zeros,pols,gain] = zpell(3,60,10,50); // フィルタの等価な線形システムを生成 num = gain * real(poly(_zeros,'s')); den = real(poly(pols,'s')); elatf = syslin('c',num,den); // 得られたフィルタをプロット bode(elatf,0.01,100); title('Analog Elliptic filter');
ボード線図はアナログフィルタでのみ使用できます.
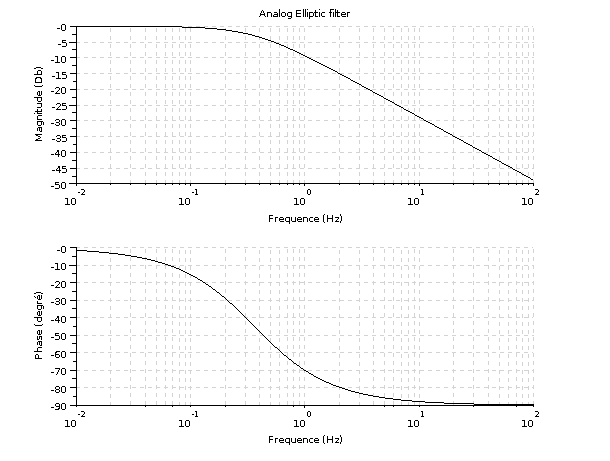
ハイパス,バンドパスまたはバンドストップフィルタを設計したい場合, ローパスフィルタをまず設計した後,このローパスフィルタを trans関数により変換します.
デジタル楕円フィルタを設計
次に,デジタル系ローパス楕円フィルタを作成する方法に着目します.
以下の2種類のデジタルフィルタを作成することができます:
IIR (Infinite Impulse Response).
このようなフィルタを作成する際,以下の関数を使用できます:
FIR (Finite Impulse Response).
このようなフィルタを作成する際,以下の関数を使用できます:
以下のデモでは,iir 関数を使用します.
Order = 2; // フィルタの次数 Fs = 1000; // サンプル周期 Fcutoff = 40; // カットオフ周波数 // ローパス楕円フィルタを設計 hz = iir(Order,'lp','ellip',[Fcutoff/Fs/2 0],[0.1 0.1]); // フィルタの周波数応用を計算 [frq,repf]=repfreq(hz,0:0.001:0.5); [db_repf, phi_repf] = dbphi(repf); // デジタルフィルタのボード線図に類似の図をプロット subplot(2,1,1); plot2d(Fs*frq,db_repf); xtitle('Obtained Frequency Response (Magnitude)'); subplot(2,1,2); plot2d(Fs*frq,phi_repf); xtitle('Obtained Frequency Response (Phase in degree)');
以下にデジタル楕円フィルタの表現を示します.
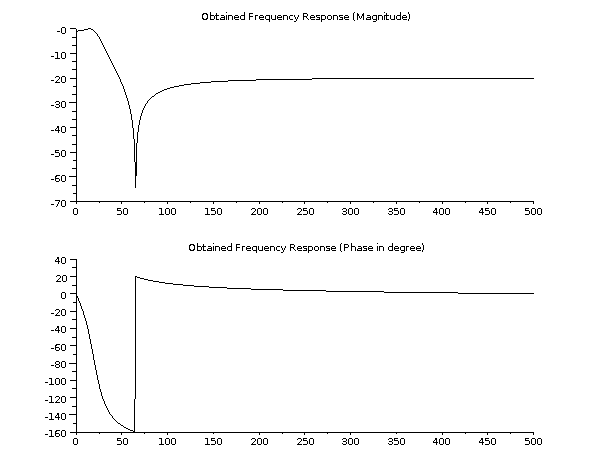
フィルタを位相および振幅で表すには, まずdbphi関数により離散インパルス応答を 振幅および位相に変換する必要があります. この変換は,正規化された周波数の集合を用いて行われます.
デジタルフィルタにより信号をフィルタ処理する
フィルタの設計は最初の一歩です.設計が完了した後,このフィルタは 信号を変換する際に使用されます. 例えば何らかのノイズを取り除くために使用されます.
以下の例では、ガウスノイズをフィルタ処理します.
rand('normal'); Input = rand(1,1000); // ランダムガウスノイズを生成 t = 1:1000; sl= tf2ss(hz); // 伝達関数から状態空間表現に変換 y = flts(Input,sl); // 信号をフィルタ subplot(2,1,1); plot(t,Input); xtitle('The gaussian noise','t','y'); subplot(2,1,2); plot(t,y); xtitle('The filtered gaussian noise','t','y');
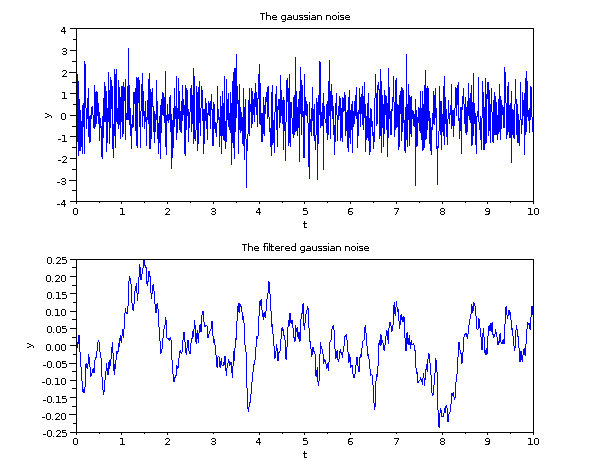
以下にフィルタ処理の前後の信号をプロットします.
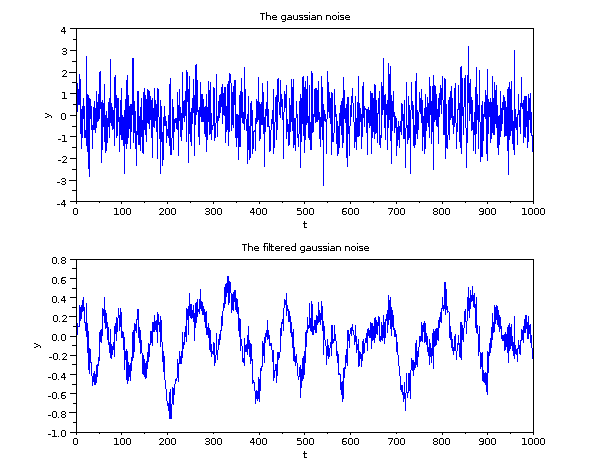
結果を見てわかるように,ノイズの高周波成分は取り除かれ, 低周波成分のみが残っています. この信号はまだノイジーですが,主に低周波域が含まれています.
アナログフィルタにより信号をフィルタ処理
アナログフィルタにより信号をフィルタ処理するには,以下の2種類の方法があります:
rand('normal'); Input = rand(1,1000); // ランダムなガウスノイズを生成 n = 1:1000; // 標本インデックス eldtf = dscr(elatf,1/100); //線形フィルタの離散化 y = flts(Input,eldtf); // 信号をフィルタ処理 subplot(2,1,1); plot(n,Input); xtitle('The gaussian noise','n','y'); subplot(2,1,2); plot(n,y); xtitle('The filtered gaussian noise','n','y');
ここで, dscr + flts の方法によりフィルタ処理する前後の信号を以下にプロットします.
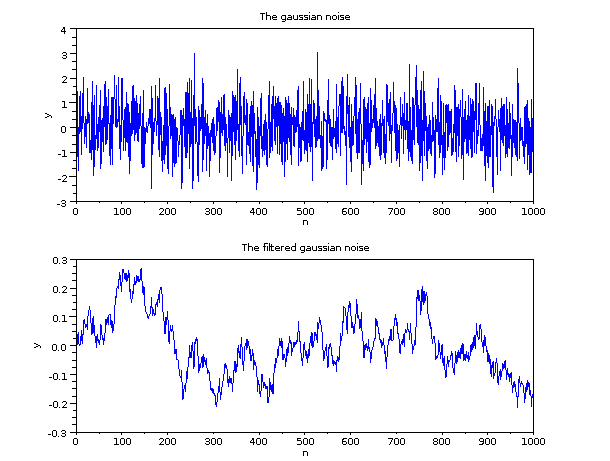
次に, csim関数を使用します.
rand('normal'); Input = rand(1,1000); // Pランダムなガウスノイズを生成 t = 1:1000; t = t*0.01; // 標本インデックスを時間刻みに変換 y = csim(Input,t,elatf); // 信号をフィルタ処理 subplot(2,1,1); plot(t,Input); xtitle('The gaussian noise','t','y'); subplot(2,1,2); plot(t,y); xtitle('The filtered gaussian noise','t','y');
以下に csimの方法によりフィルタ処理する前後の信号を以下にプロットします.
dscr + flts による方法を csim による方法の主な違いを以下に示します : dscr + flts は標本を使用しますが,csim 関数は時間刻みを使用します.
参照
| Report an issue | ||
| << How to | How to | identification >> |