Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
However, this page did not exist in the previous stable version.
Rootfinding
This feature finds roots of continuous functions for Zero-crossing Blocks.
Description
Some problems require zero crossing detection of continuous functions (for instance, regulation systems), also named rootfinding. This feature is common to all solvers, and is realized by following the same process.
Each Zero-crossing Block defines one of these functions, noted g(t).
Generally, the feature only finds roots of odd multiplicity, corresponding to changes in sign of g(t). If a user root function has a root of even multiplicity (no sign change), it will probably be missed. If such a root is desired, the user should reformulate the root function so that it changes sign at the desired root.
The basic scheme used is to check for sign changes of any g(t) over each time step taken, and then (when a sign change is found) to home in on the root (or roots) with a modified secant method.
After suitable checking and adjusting has been done, the roots are to be sought within [tlo, thi] . A loop is entered to locate the root to within a rather tight tolerance, given by the unit roudoff, the current time and the step size.
We then determine which root function is more likely to have its roots occur first by comparing the secant method values, and set a new value tmid and restrain the research interval to either [tlo, tmid] or [tmid, thi] , following which does the sign change occur in.
Since the tolerance depends on the step size, the smaller it is, the more accurate the homing in will be.
Examples and Overhead
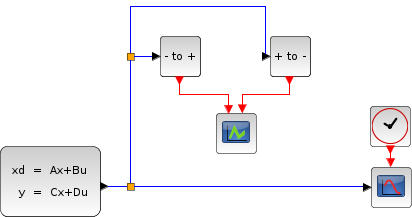
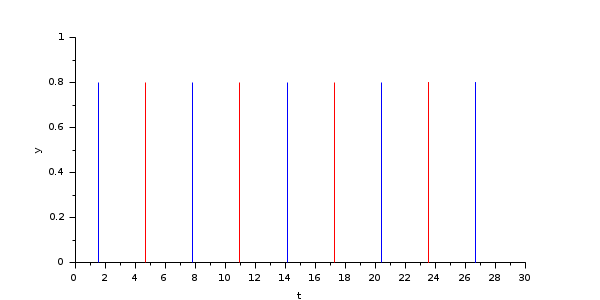
Simple example of a Sine crossing zero several times:
// Import the diagram and set the ending time loadScicos(); loadXcosLibs(); importXcosDiagram("SCI/modules/xcos/demos/Threshold_ZeroCrossing.zcos"); // Start the timer, launch the simulation and display time tic(); try xcos_simulate(scs_m, 4); catch disp(lasterror()); end t = toc(); disp(t, "Time for LSodar:");
The blue bars represent the "positive to negative" zero crossings, while the red ones are for "negative to positive".
Now, in the two following scripts, we test the computational overhead of the rootfinding with LSodar:
First, a Sine function that crosses zero every π period: Open the script
Time with rootfinding:
15.021
Time without rootfinding:
10.573
Then, a simple straight line that crosses zero only once, in the middle of the interval: Open the script
Time with rootfinding:
0.114
Time without rootfinding:
0.09
Following the number of zero crossings, the aspect of the function near these crossings, the tolerances, ..., the computational overhead ranges between 25% and 45%.
See Also
Bibliography
| Report an issue | ||
| << Implicit Runge-Kutta 4(5) | Solveurs | Comparisons >> |