Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
frep2tf
transfer function realization from frequency response
Calling Sequence
[h [,err]]=frep2tf(frq,repf,dg [,dom,tols,weight])
Arguments
- frq
vector of frequencies in Hz.
- repf
vector of frequency response
- dg
degree of linear system
- dom
time domain (
'c'or'd'ordt)- tols
a vector of size 3 giving the relative and absolute tolerance and the maximum number of iterations (default values are
rtol=1.e-2; atol=1.e-4, N=10).- weight
vector of weights on frequencies
- h
SISO transfer function
- err
error (for example if
dom='c'sum(abs(h(2i*pi*frq) - rep)^2)/size(frq,*))
Description
Frequency response to transfer function conversion. The order of h
is a priori given in dg which must be provided.
The following linear system is solved in the least square sense.
weight(k)*(n( phi_k) - d(phi_k)*rep_k)=0, k=1,..,n
where phi_k= 2*%i*%pi*frq when dom='c' and phi_k=exp(2*%i*%pi*dom*frq if not. If the weight vector is not given a default
penalization is used (when dom='c').
A stable and minimum phase system can be obtained by using function factors.
Examples
s=poly(0,'s'); h=syslin('c',(s-1)/(s^3+5*s+20)) frq=0:0.05:3; repf=repfreq(h,frq); clean(frep2tf(frq,repf,3))
Sys=ssrand(1,1,10); frq=logspace(-3,2,200); [frq,rep]=repfreq(Sys,frq); //Frequency response of Sys [Sys2,err]=frep2tf(frq,rep,10); Sys2=clean(Sys2) //Sys2 obtained from freq. resp of Sys [frq,rep2]=repfreq(Sys2,frq); //Frequency response of Sys2 clf(); bode(frq,[rep;rep2]) //Responses of Sys and Sys2 [gsort(spec(Sys('A'))), gsort(roots(Sys2('den')))] //poles
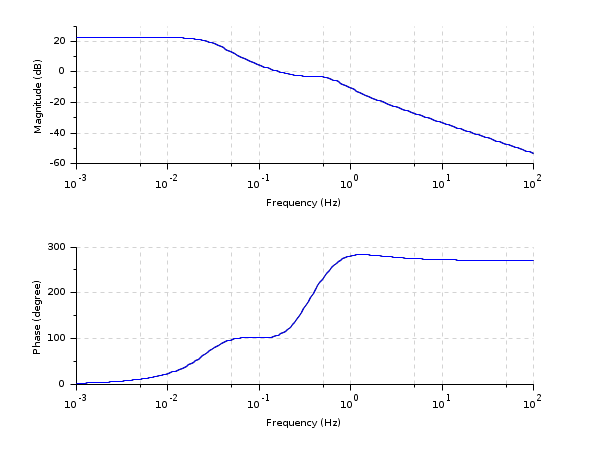
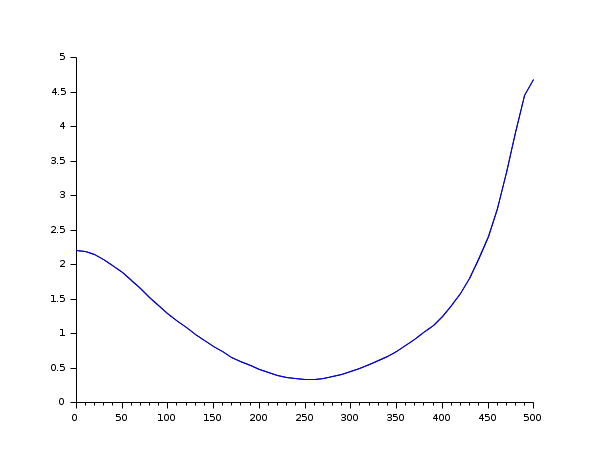
dom=1/1000; // Sampling time z=poly(0,'z'); h=syslin(dom,(z^2+0.5)/(z^3+0.1*z^2-0.5*z+0.08)) frq=(0:0.01:0.5)/dom; repf=repfreq(h,frq); [Sys2,err]=frep2tf(frq,repf,3,dom); [frq,rep2]=repfreq(Sys2,frq); //Frequency response of Sys2 clf(); plot2d1("onn",frq',abs([repf;rep2])');
See Also
| Report an issue | ||
| << des2tf | formal_representation | markp2ss >> |