datafit

Arguments

imp

scalar argument used to set the trace mode. imp=0 nothing (execpt errors) is reported, imp=1 initial and final reports, imp=2 adds a report per iteration, imp>2 add reports on linear search.

Warning: most of these reports are written on the Scilab standard output.

G

function descriptor (e=G(p,z), e: ne x 1, p: np x 1, z: nz x 1)

DG

partial of G wrt p function descriptor (optional; S=DG(p,z), S: ne x np)

Z

matrix [z_1,z_2,...z_n] where z_i (nz x 1) is the ith measurement

W

weighting matrix of size ne x ne (optional; defaut no ponderation)

contr

'b',binf,bsup with binf and bsup real vectors with same dimension as p0. binf and bsup are lower and upper bounds on p.

p0

initial guess (size np x 1)

algo

'qn' or 'gc' or 'nd' . This string stands for quasi-Newton (default), conjugate gradient or non-differentiable respectively. Note that 'nd' does not accept bounds on x ).

df0

real scalar. Guessed decreasing of f at first iteration. (df0=1 is the default value).

mem :

integer, number of variables used to approximate the Hessian, (algo='gc' or 'nd'). Default value is around 6.

stop

sequence of optional parameters controlling the convergence of the algorithm. stop= 'ar',nap, [iter [,epsg [,epsf [,epsx]]]]

"ar"

reserved keyword for stopping rule selection defined as follows:

nap

maximum number of calls to fun allowed.

iter

maximum number of iterations allowed.

epsg

threshold on gradient norm.

epsf

threshold controlling decreasing of f

epsx

threshold controlling variation of x. This vector (possibly matrix) of same size as x0 can be used to scale x.

"in"

reserved keyword for initialization of parameters used when fun in given as a Fortran routine (see below).

p

Column vector, optimal solution found

err

scalar, least square error.

Description

datafit is used for fitting data to a model. For a given function G(p,z), this function finds the best vector of parameters p for approximating G(p,z_i)=0 for a set of measurement vectors z_i. Vector p is found by minimizing G(p,z_1)'WG(p,z_1)+G(p,z_2)'WG(p,z_2)+...+G(p,z_n)'WG(p,z_n)

Examples

//generate the data
function y=FF(x, p)
  y=p(1)*(x-p(2))+p(3)*x.*x
endfunction

X=[];
Y=[];
pg=[34;12;14] //parameter used to generate data
for x=0:.1:3
  Y=[Y,FF(x,pg)+100*(rand()-.5)];
  X=[X,x];
end
Z=[Y;X];

//The criterion function
function e=G(p, z),
  y=z(1),x=z(2);
  e=y-FF(x,p),
endfunction

//Solve the problem
p0=[3;5;10]    
[p,err]=datafit(G,Z,p0);

scf(0);clf()
plot2d(X,FF(X,pg),5) //the curve without noise
plot2d(X,Y,-1)  // the noisy data
plot2d(X,FF(X,p),12) //the solution

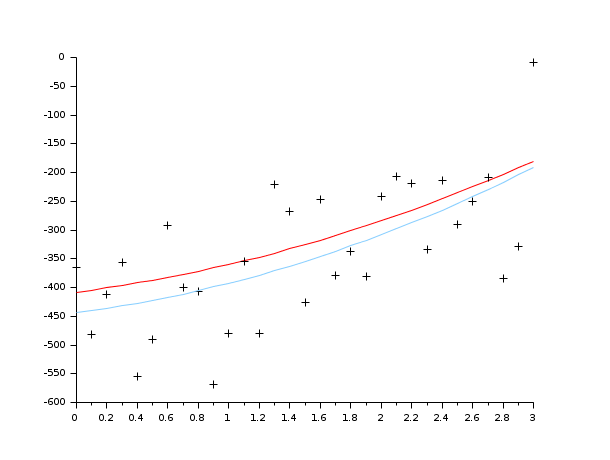
//generate the data
function y=FF(x, p)
  y=p(1)*(x-p(2))+p(3)*x.*x
endfunction

//the gradient of the criterion function
function s=DG(p, z),
  a=p(1),b=p(2),c=p(3),y=z(1),x=z(2),
  s=-[x-b,-a,x*x]
endfunction

function e=G(p, z),
  y=z(1),x=z(2);
  e=y-FF(x,p),
endfunction

X=[];Y=[];
pg=[34;12;14]
for x=0:.1:3
  Y=[Y,FF(x,pg)+100*(rand()-.5)];
  X=[X,x];
end
Z=[Y;X];

p0=[3;5;10]    
[p,err]=datafit(G,DG,Z,p0);
scf(1);
clf()
plot2d(X,FF(X,pg),5) //the curve without noise
plot2d(X,Y,-1)  // the noisy data
plot2d(X,FF(X,p),12) //the solution

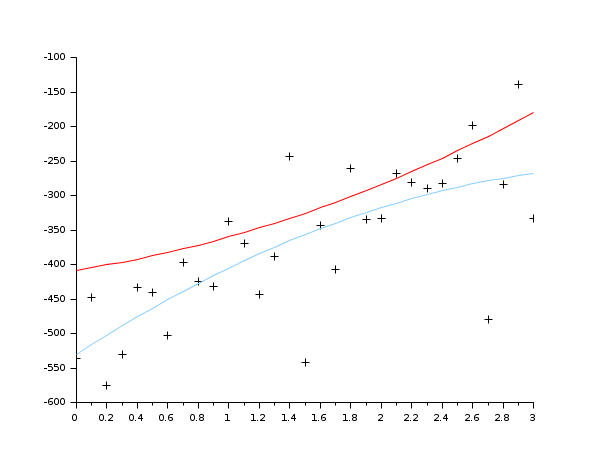
//generate the data
function y=FF(x, p)
  y=p(1)*(x-p(2))+p(3)*x.*x
endfunction

//the gradient of the criterion function
function s=DG(p, z),
  a=p(1),b=p(2),c=p(3),y=z(1),x=z(2),
  s=-[x-b,-a,x*x]
endfunction

function e=G(p, z),
  y=z(1),x=z(2);
  e=y-FF(x,p),
endfunction

X=[];Y=[];
pg=[34;12;14]
for x=0:.1:3
  Y=[Y,FF(x,pg)+100*(rand()-.5)];
  X=[X,x];
end
Z=[Y;X];

p0=[3;5;10]    

// Add some bounds on the estimate of the parameters
// We want positive estimation (the result will not change)
[p,err]=datafit(G,DG,Z,'b',[0;0;0],[%inf;%inf;%inf],p0,algo='gc');
scf(1);
clf()
plot2d(X,FF(X,pg),5) //the curve without noise
plot2d(X,Y,-1)  // the noisy data
plot2d(X,FF(X,p),12) //the solution

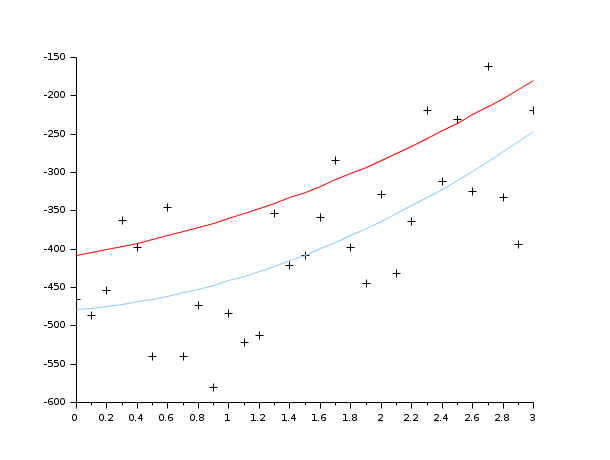
See Also

• lsqrsolve — minimize the sum of the squares of nonlinear functions, levenberg-marquardt algorithm
• optim — non-linear optimization routine
• leastsq — Solves non-linear least squares problems