Arguments

A

a real or complex vector or real or complex array (vector, matrix or N-D array).

X

a real or complex array with same shape as A.

sign

an integer. with possible values 1 or -1. Select direct or inverse transform. The default value is -1 (direct transform).

option

a character string. with possible values "symmetric" or "nonsymmetric". Indicates if A is symmetric or not. If this argument is omitted the algorithm automatically determines if A is symmetric or not. See the Description part for details.

selection

a vector containing index on A array dimensions. See the Description part for details.

dims

a vector of positive numbers with integer values, or a vector of positive integers. See the Description part for details.

Each element must be a divisor of the total number of elements of A.

The product of the elements must be less than the total number of elements of A.

incr

a vector of positive numbers with integer values, or a vector of positive integers. See the Description part for details.

incr must have the same number of elements than dims.

Each element must be a divisor of the total number of elements of A.

The incr elements must be in strictly increasing order.

Description

Short syntax

direct

X=fft(A,-1 [,option]) or X=fft(A [,option]) gives a direct transform.

single variate

If A is a vector a single variate direct FFT is computed that is: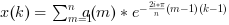

(the -1 argument refers to the sign of the exponent..., NOT to "inverse"),

multivariate

If A is a matrix or a multidimensional array a multivariate direct FFT is performed.

inverse

X=fft(A,1) or X=ifft(A)performs the inverse normalized transform, such thatA==ifft(fft(A)).

single variate

If A is a vector a single variate inverse FFT is computed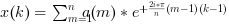

multivariate

If a is a matrix or or a multidimensional array a multivariate inverse FFT is performed.

Long syntax for FFT along specified dimensions

• X=fft(A,sign,selection [,option]) allows to perform efficiently all direct or inverse fft of the "slices" of A along selected dimensions.

  For example, if A is a 3-D array X=fft(A,-1,2) is equivalent to:

  for i1=1:size(A,1)
    for i3=1:size(A,3)
      X(i1,:,i3)=fft(A(i1,:,i3),-1);
    end
  end

  and X=fft(A,-1,[1 3]) is equivalent to:

  for i2=1:size(A,2)
    X(:,i2,:)=fft(A(:,i2,:),-1);
  end

• X=fft(A,sign,dims,incr [,option]) is a previous syntax that also allows to perform all direct or inverse fft of the slices of A along selected dimensions.

  For example, if A is an array with n1*n2*n3 elements X=fft(A,-1,n1,1) is equivalent to X=fft(matrix(A,[n1,n2,n3]),-1,1). and X=fft(A,-1,[n1 n3],[1 n1*n2]) is equivalent to X=fft(matrix(A,[n1,n2,n3]),-1,[1,3]).

Using option argument This argument can be used to inform the fft algorithm about the symmetry of A or of all its "slices". An N-D array B with dimensions n1, ..., np is conjugate symmetric for the fft if and only if B==conj(B([1 n1:-1:2],[1 n2:-1:2],...,[1 np:-1:2])) .In such a case the result X is real and an efficient specific algorithm can be used.

• "symmetric" that value causes fft to treat A or all its "slices" conjugate symmetric. This option is useful to avoid automatic determination of symmetry or if A or all its "slices" are not exactly symmetric because of round-off errors.
• "nonsymmetric" that value causes fft not to take care of symmetry. This option is useful to avoid automatic determination of symmetry.
• unspecified If the option is omitted the fft algorithm automatically checks for exact symmetry.

Optimizing fft

Remark: fftw function automatically stores his last parameters in memory to re-use it in a second time. This improves greatly the time computation when consecutives calls (with same parameters) are performed.

It is possible to go further in fft optimization using get_fftw_wisdom, set_fftw_wisdom functions.

Algorithms

This function uses the fftw3 library.

Examples

1-D fft

//Frequency components of a signal
//----------------------------------
// build a noised signal sampled at 1000hz  containing  pure frequencies
// at 50 and 70 Hz
sample_rate=1000;
t = 0:1/sample_rate:0.6;
N=size(t,'*'); //number of samples
s=sin(2*%pi*50*t)+sin(2*%pi*70*t+%pi/4)+grand(1,N,'nor',0,1);

y=fft(s);

//s is real so the fft response is conjugate symmetric and we retain only the first N/2 points
f=sample_rate*(0:(N/2))/N; //associated frequency vector
n=size(f,'*')
clf()
plot(f,abs(y(1:n)))

2-D fft

----------------------------------
A = zeros(256,256);
A(5:24,13:17) = 1;
X = fftshift(fft(A));
set(gcf(),"color_map",jetcolormap(128));
clf;grayplot(0:255,0:255,abs(X)')

mupliple fft

//simple case, 3 1-D fft at a time
N=2048;
t=linspace(0,10,2048);
A=[2*sin(2*%pi*3*t)+ sin(2*%pi*3.5*t)
  10*sin(2*%pi*8*t)
   sin(2*%pi*0.5*t)+4*sin(2*%pi*0.8*t)];
X=fft(A,-1,2);

fs=1/(t(2)-t(1));
f=fs*(0:(N/2))/N; //associated frequency vector
clf;plot(f(1:100)',abs(X(:,1:100))')
legend(["3 and 3.5 Hz","8 Hz","0.5 and 0.8 Hz"],"in_upper_left")

// 45  3-D fft at a time
Dims=[5 4 9 5 6];
A=matrix(rand(1,prod(Dims)),Dims);

y=fft(A,-1,[2 4 5]);

//equivalent (but less efficient code)
y1=zeros(A);
for i1=1:Dims(1)
  for i3=1:Dims(3)
    ind=list(i1,:,i3,:,:);
    y1(ind(:))=fft(A(ind(:)),-1);
  end
end

//Using explicit formula for  1-D discrete Fourier transform
//------------------------------------------------
function xf=DFT(x, flag);
  n=size(x,'*');
  //Compute the n by n Fourier matrix
  if flag==1 then,//backward transformation
    am=exp(2*%pi*%i*(0:n-1)'*(0:n-1)/n);
  else //forward transformation
    am=exp(-2*%pi*%i*(0:n-1)'*(0:n-1)/n);
  end
  xf=am*matrix(x,n,1);//dft
  xf=matrix(xf,size(x));//reshape
  if flag==1 then,xf=xf/n;end
endfunction

//Comparison with the fast Fourier algorithm
a=rand(1,1000);
norm(DFT(a,1) - fft(a,1))
norm(DFT(a,-1) - fft(a,-1))

timer();DFT(a,-1);timer()
timer();fft(a,-1);timer()

See Also

• corr — correlation, covariance
• fftw_flags — set method for fft planner algorithm selection
• get_fftw_wisdom — return fftw wisdom
• set_fftw_wisdom — set fftw wisdom
• fftw_forget_wisdom — Reset fftw wisdom

Bibliography

Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation