Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
Runge-Kutta 4(5)
Runge-Kutta est un solveur numérique fournissant une méthode explicite efficace pour résoudre des Problèmes à Valeur Initiale d'Equations Différentielles Ordinarires (EDOs).
Description
Appelé par xcos, Runge-Kutta est un solveur numérique fournissant une méthode efficace et stable pour résoudre des Problèmes à Valeur Initiale de la forme :

CVode et IDA utilisent un pas variable dans l'intégration.
Le défaut de cela est l'imprévisibilité du temps de calcul. Avec Runge-Kutta, on ne s'adapte pas à la complexité du problème, mais on garantit un temps de calcul stable.
Cette méthode est explicite, donc non concernée par les itérations fonctionnelles ou de Newton, et est déconseillée pour les problèmes raides.
C'est une amélioration de la méthode d'Euler, qui approxime yn+1 en tronquant le développement de Taylor.
Par convention, pour utiliser des pas fixes, le programme commence par calculer un pas h qui approche le paramère de simulation max step size.
Une différence notable de Runge-Kutta par rapport à Sundials est qu'il calcule jusqu'à la dérivée quatrième de y, alors que les autres n'utilisent que des combinaisons linéaires de y et y'.
Ici, la valeur suivante est déterminée par la valeur actuelle yn plus la moyenne pondérée de quatre incréments, où chaque incrément est le produit du pas, h, et une estimation de la pente spécifiée par la fonction f(t,y) :
- k1 est l'incrément basé sur la pente au début de l'intervalle, utilisant yn (méthode d'Euler),
- k2 est l'incrément basé sur la pente au milieu de l'intervalle, utilisant yn + h*k1/2 ,
- k3 est à nouveau l'incrément basé sur la pente au milieu de l'intervalle, utilisant yn + h*k2/2
- k4 est l'incrément basé sur la pente à la fin de l'intervalle, utilisant yn + h*k3
On peut voir qu'avec les ki, on progresse dans les dérivées de yn . Donc à k4, on approxime y(4)n , faisant donc une erreur en O(h5) .
L'erreur totale est donc nombre de pas * O(h5) . Et puisque par définition nombre de pas = taille de l'intervalle / h, l'erreur totale est en O(h4) .
Cette analyse d'erreur a baptisé la méthode Runge-Kutta 4(5), O(h5) par pas, O(h4) au total.
Bien que le solveur fonctionne bien pour max step size allant juqu'à 10-3 , des erreurs d'arrondi surviennent parfois quand l'on approche 4*10-4 . En effet, le scindage de l'intervalle ne peut pas être effectué correctement et l'on obtient des résultats imprévisibles.
Exemples
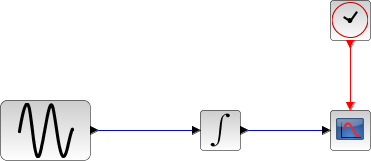
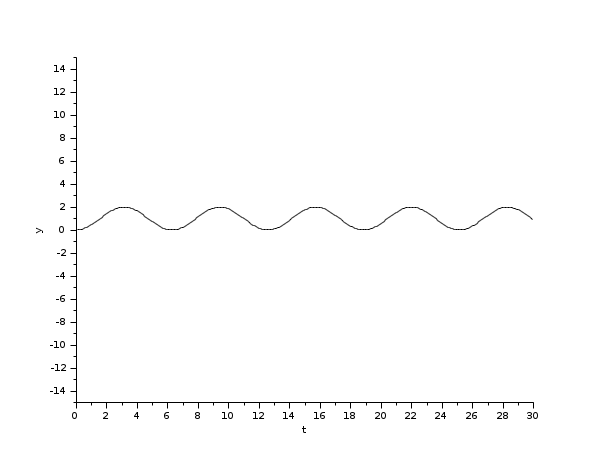
Le bloc intégrale retourne son état continu, on peut l'évaluer avec Runge-Kutta en lançant l'exemple :
// Import du diagramme et réglage du temps final loadScicos(); loadXcosLibs(); importXcosDiagram("SCI/modules/xcos/examples/solvers/ODE_Example.zcos"); scs_m.props.tf = 5000; // Sélection de Runge-Kutta et réglage de la précision scs_m.props.tol(6) = 6; scs_m.props.tol(7) = 10^-2; // Lancement du chrono, de la simulation et affichage du temps tic(); try xcos_simulate(scs_m, 4); catch disp(lasterror()); end t = toc(); disp(t, "Temps pour Runge-Kutta :");
La console Scilab affiche :
Temps pour Runge-Kutta :
8.906
Maintenant, dans le script suivant, on compare la différence de temps entre Runge-Kutta et CVode en lançant l'exemple avec les cinq solveurs tour à tour : Ouverture du script
Temps pour BDF / Newton :
18.894
Temps pour BDF / Functional :
18.382
Temps pour Adams / Newton :
10.368
Temps pour Adams / Functional :
9.815
Temps pour Runge-Kutta :
4.743
Ces résultats montrent que pour un problème non-raide, pour à peu près la même précision demandée et en forçant la même taille de pas, Runge-Kutta est plus rapide.
Voir Aussi
Bibliographie
Histoire
| Version | Description |
| 5.4.1 | Runge-Kutta 4(5) ajouté |
| Report an issue | ||
| << CVode | Solveurs | Dormand-Prince 4(5) >> |