Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
ndgrid
arrays for multidimensional function evaluation on grid
Calling Sequence
[X, Y] = ndgrid(x,y) [X, Y, Z] = ndgrid(x,y,z) [X, Y, Z, T] = ndgrid(x,y,z,t) [X1, X2, ..., Xm] = ndgrid(x1,x2,...,xm)
Arguments
- x, y, z, ...
vectors
- X, Y, Z, ...
matrices in case of 2 input arguments, or else hypermatrices
Description
This is an utility routine useful to create arrays for function
evaluation on 2, 3, ..., n dimensional grids. For instance in 2d, a grid
is defined by two vectors, x and y
of length nx and ny, and you want to evaluate a function (says
f) on all the grid points, that is on all the points
of coordinates (x(i),y(j)) with
i=1,..,nx and j=1,..,ny. In this
case, this function can compute the two matrices X,Y of
size nx x ny such that :
X(i,j) = x(i) for all i in [1,nx] Y(i,j) = y(j) and j in [1,ny]
and the evaluation may be done with Z=f(X,Y) (at
the condition that you have coded f for evaluation on
vector arguments, which is done (in general) by using the element-wise
operators .*, ./ and
.^ in place of *,
/ and ^).
In the 3d case, considering 3 vectors x,y,z of
length nx, ny and nz, X,Y,Z are 3 hypermatrices of size
nx x ny x nz such that :
X(i,j,k) = x(i) Y(i,j,k) = y(j) for all (i,j,k) in [1,nx]x[1,ny]x[1,nz] Z(i,j,k) = z(k)
In the general case of m input arguments x1, x2, ..,
xm
,then the m output arguments X1, X2, ..,
Xm
are hypermatrices of size nx1 x nx2 x ... x
nxm
and :
Xj(i1,i2,...,ij,...,im) = xj(ij) for all (i1,i2,...,im) in [1,nx1]x[1,nx2]x...x[1,nxm]
Examples
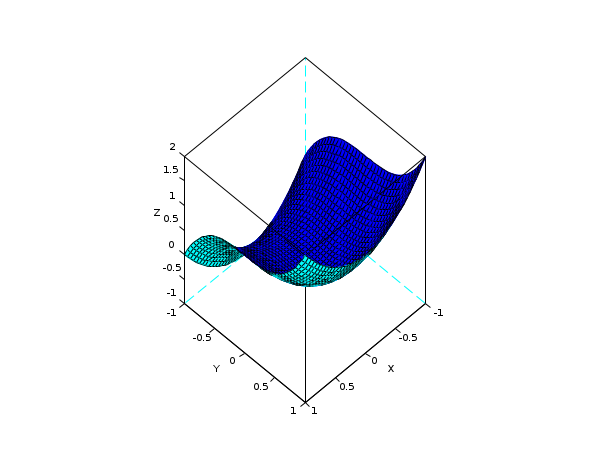
// create a simple 2d grid nx = 40; ny = 40; x = linspace(-1,1,nx); y = linspace(-1,1,ny); [X,Y] = ndgrid(x,y); // compute a function on the grid and plot it //deff("z=f(x,y)","z=128*x.^2 .*(1-x).^2 .*y.^2 .*(1-y).^2"); deff("z=f(x,y)","z=x.^2 + y.^3") Z = f(X,Y); clf() plot3d(x,y,Z, flag=[2 6 4]); show_window()
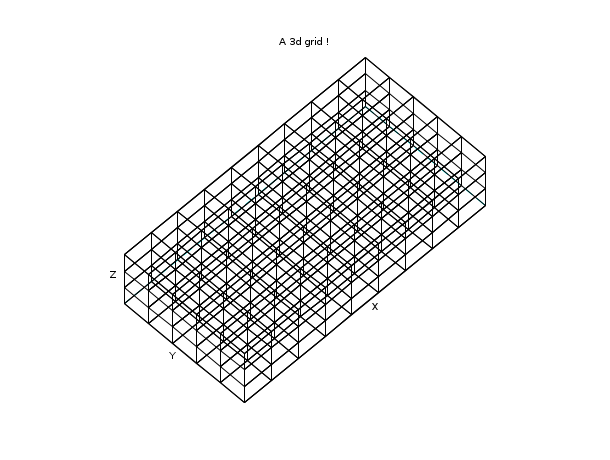
// create a simple 3d grid nx = 10; ny = 6; nz = 4; x = linspace(0,2,nx); y = linspace(0,1,ny); z = linspace(0,0.5,nz); [X,Y,Z] = ndgrid(x,y,z); // try to display this 3d grid ... XF=[]; YF=[]; ZF=[]; for k=1:nz [xf,yf,zf] = nf3d(X(:,:,k),Y(:,:,k),Z(:,:,k)); XF = [XF xf]; YF = [YF yf]; ZF = [ZF zf]; end for j=1:ny [xf,yf,zf] = nf3d(matrix(X(:,j,:),[nx,nz]),... matrix(Y(:,j,:),[nx,nz]),... matrix(Z(:,j,:),[nx,nz])); XF = [XF xf]; YF = [YF yf]; ZF = [ZF zf]; end clf() plot3d(XF,YF,ZF, flag=[0 6 3], leg="X@Y@Z") xtitle("A 3d grid !"); show_window()
See Also
- kron — Kronecker product (.*.)
| Report an issue | ||
| << meshgrid | Elementary matrices | ones >> |