ode

Аргументы

y0

вектор или матрица вещественных значений, начальные условия.

t0

вещественный скаляр, начальное время.

t

вещественный вектор, моменты времени для которых находится решение.

f

внешняя функция (функция, строка или список), правая сторона дифференциального уравнения.

type

строка, тип используемой программы решения. Имеются следующие типы программ решения: "adams", "stiff", "rk", "rkf", "fix", "discrete", "roots".

rtol

вещественная константа либо вещественный вектор того же размера, что и y, относительный допуск.

atol

вещественная константа либо вещественный вектор того же размера, что и y, абсолютный допуск.

jac

внешняя функция (функция, строка или список), якобиан функции f.

w, iw

вещественные векторы (ВХОДНЫЕ/ВЫХОДНЫЕ).

ng

целое число.

g

внешняя функция (функция, символьная строка или список).

k0

целое число (начальное время).

kvect

целочисленный вектор.

y

вещественный вектор или матрица (ВЫХОДНАЯ).

rd

вещественный вектор (ВЫХОДНОЙ).

Описание

ode решает явные обыкновенные дифференциальные уравнения, определённые как:

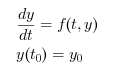
Это интерфейс для различных программ решения, в частности для ODEPACK.

В данной справке описывается использование ode для стандартных явных систем ОДУ.

Самый простой способ вызова ode: y = ode(y0, t0, t, f), где y0 - вектор начальных условий, t0 - начальное время, t - вектор моментов времени, для которых вычисляется решение y и y - матрица векторов решения y=[y(t(1)),y(t(2)),...].

Входной аргумент f определяет правую сторону дифференциального уравнения первого порядка. Этот аргумент является функцией с определённым заголовком.

• Если f является Scilab-функцией, то её последовательность вызова должна быть:

  ydot = f(t,y)
   

  где t - вещественный скаляр (время), а y - вещественный вектор (состояние) и ydot - вещественный вектор (производная первого порядка dy/dt).

• Если f - строка, то это - имя компилированной процедуры Fortran или функции C. Например, если вызывается ode(y0, t0, t, "fex"), то вызывается подпрограмма fex.

  Процедура Fortran должна иметь заголовок:

  fex(n,t,y,ydot)
   

  где n - целое число, t -- скаляр двойной точности, y и ydot - векторы двойной точности.

  Функция C должна иметь заголовок:

  fex(int *n,double *t,double *y,double *ydot)
   

  где t - время, y - состояние, а ydot - производная состояния (dy/dt).

  Эта внешняя функция может быть собрана способом, независящим от ОС, используя ilib_for_link и динамически связана с Scilab с помощью функции link.

• Может случиться, что симулятору f потребуются дополнительные аргументы. В этом случае можно использовать следующую возможность. Аргумент f может также быть списком lst=list(simuf,u1,u2,...un), где simuf является Scilab-функцией с синтаксисом: ydot = f(t,y,u1,u2,...,un), а u1, u2, ..., un - дополнительные аргументы, автоматически передаваемые симулятору simuf.

Функция f может возвращать вместо вектора матрицуp x q. С этой матричной нотацией решается система n=p+q ОДУ dY/dt=F(t,Y), где Y - матрица p x q. Затем начальные условия, Y0, должны быть так же матрицей p x q, а результат ode - матрицей p x q(T+1) [Y(t_0),Y(t_1),...,Y(t_T)].

Допуски rtol и atol являются порогами для относительной и абсолютной оценённых ошибок. Оценённая ошибка y(i) равна: rtol(i)*abs(y(i))+atol(i) и интегрирование выполняется пока эта ошибка мала для каждого из элементов состояния. Если rtol и/или atol является константой, то rtol(i) и/или atol(i) являются набором констант. Значения по умолчанию для rtol и atol соответственно равны rtol=1.d-5 и atol=1.d-7 для большинства программ решения, а для "rfk" и "fix" rtol=1.d-3 и atol=1.d-4.

Для жёстких задач лучше указывать якобиан функции правой стороны в качестве необязательного аргумента jac. Якобиан является внешней функцией, т. е. функцией со специальным синтаксисом, либо именем процедуры Fortran или функции C (символьная строка) с определённой последовательностью вызова, либо списком.

• Если jac является функцией, то синтаксис должен быть J=jac(t,y), где t -- вещественный скаляр (время), а y - вещественный вектор (состояние). Результирующая матрица J должна вычислять df/dx, т. е. J(k,i) = dfk/dxi, где fk - k-тый элемент f.

• Если jac является символьной строкой, то она ссылается на имя процедуры Fortran или функции C.

  Процедура Fortran должна иметь заголовок:

  subroutine fex(n,t,y,ml,mu,J,nrpd)
  integer n,ml,mu,nrpd
  double precision t,y(*),J(*)
   

  Функция C должна иметь заголовок:

  void fex(int *n,double *t,double *y,int *ml,int *mu,double *J,int *nrpd,)
   

  В большинстве случаев не нужно ссылаться на ml, mu и nrpd.

• Если jac является списком, то для f применяются те же договорённости.

Необязательные аргументы w и iw являются векторами для хранения информации, возвращаемой подпрограммой интегрирования (см. ode_optional_output). Когда эти векторы указываются с правой стороны ode, интегрирование начинается заново с теми же параметрами, что и до остановки.

Программам решения ODEPACK можно передать больше опций с помощью переменной %ODEOPTIONS. See odeoptions.

Программы решения

Тип задачи, которую надо решить и используемый метод зависят от значения первого необязательного аргумента type, который может быть одной из следующих строк:

<не задано>:

Программа решения lsoda из пакета ODEPACK вызывается по умолчанию. Она автоматически выбирает между нежёстким методом прогноза-исправления Адамса (predictor-corrector Adams method) и жёстким методом обратной дифференциальной формулой (ОДФ) ( Backward Differentiation Formula (BDF) method). Изначально она применяет нежёсткий метод и динамически проверяет данные для того, чтобы решить какой метод использовать.

"adams":

Используется для нежёстких задач. Вызывается программа решения lsode из пакета ODEPACK, и она использует метод Адамса.

"stiff":

Это для жёстких задач. Вызывается программа решения lsode из пакета ODEPACK, и она использует метод ОДФ.

"rk":

Адаптивный метод Рунге-Кутты 4-го порядка (RK4).

"rkf":

Используется программа Шампайна и Уотса (Shampine и Watts), основанная на методе Рунге-Кутты-Фелберга пары 4 и 5-го порядка (RKF45). Она для нежёстких и среднежёстких задач, когда получаемые вычисления не дороги. Этот метод не следует, в общем случае, использовать, если пользователь требует высокую точность.

"fix":

Та же программа решения, что и "rkf", но пользовательский интерфейс очень прост, т. е. программе решения могут быть переданы только параметры rtol и atol. Это самый простой метод для пробы.

"root":

Программа решения ОДУ с возможностью нахождения корней. Используется программа решения lsodar из пакета ODEPACK. Она является вариантом программы решения lsoda, где она ищет корни заданной векторной функции. См. справку по ode_root.

"discrete":

Моделирование дискретного времени. См. справку по ode_discrete.

Примеры

В следующем примере мы решим обыкновенное дифференциальное уравнение dy/dt=y^2-y*sin(t)+cos(t) с начальным условием y(0)=0. Используем программу решения по умолчанию.

function ydot=f(t, y)
    ydot=y^2-y*sin(t)+cos(t)
endfunction
y0=0;
t0=0;
t=0:0.1:%pi;
y = ode(y0,t0,t,f);
plot(t,y)

В следующем примере мы решаем уравнение dy/dt=A*y. Точное решение равно y(t)=expm(A*t)*y(0), где expm - матричная экспонента. Неизвестное равно матрице y(t) размером 2 на 1.

function ydot=f(t, y)
    ydot=A*y
endfunction
function J=Jacobian(t, y)
    J=A
endfunction
A=[10,0;0,-1];
y0=[0;1];
t0=0;
t=1;
ode("stiff",y0,t0,t,f,Jacobian)
// Сравним с точным решением:
expm(A*t)*y0

В следующем примере мы решаем ОДУ dx/dt = A*x(t) + B*u(t) с u(t)=sin(omega*t). Обратите внимание, что дополнительные аргументы f: A, u, B, omega передаются в f в списке.

function xdot=linear(t, x, A, u, B, omega)
    xdot=A*x+B*u(t,omega)
endfunction
function ut=u(t, omega)
    ut=sin(omega*t)
endfunction
A=[1 1;0 2];
B=[1;1];
omega=5;
y0=[1;0];
t0=0;
t=[0.1,0.2,0.5,1];
ode(y0,t0,t,list(linear,A,u,B,omega))

В следующем примере мы решим дифференциальное уравнение Риккати dX/dt=A'*X + X*A - X'*B*X + C, где начальное условие X(0) является единичной матрицей 2 на 2.

function Xdot=ric(t, X, A, B, C)
    Xdot=A'*X+X*A-X'*B*X+C
endfunction
A=[1,1;0,2];
B=[1,0;0,1];
C=[1,0;0,1];
y0=eye(A);
t0=0;
t=0:0.1:%pi;
X = ode(y0,t0,t,list(ric,A,B,C))

В следующем примере мы решаме дифференциальное уравнение dY/dt=A*Y, где неизвестная Y(t) является матрицей 2 на 2. Точное решение равно expm Y(t)=expm(A*t), где expm -- матричная экспонента.

function ydot=f(t, y, A)
    ydot=A*y;
endfunction
A=[1,1;0,2];
y0=eye(A);
t0=0;
t=1;
ode(y0,t0,t,list(f,A))
// Сравнение с точным решением
expm(A*t)
ode("adams",y0,t0,t,f)

С компилятором

Следующий пример требует компилятор C.

// ---------- Простое одномерное ОДУ (внешняя функция на языке C)
ccode=['#include <math.h>'
       'void myode(int *n,double *t,double *y,double *ydot)'
       '{'
       '  ydot[0]=y[0]*y[0]-y[0]*sin(*t)+cos(*t);'
       '}']
mputl(ccode,TMPDIR+'/myode.c') // создаём C-файл
// Компилируем
ilib_for_link('myode','myode.c',[],'c',TMPDIR+'/Makefile',TMPDIR+'/loader.sce');
exec(TMPDIR+'/loader.sce') // пошаговая компоновка
y0=0;
t0=0;
t=0:0.1:%pi;
y = ode(y0,t0,t,'myode');

Смотрите также

• ode_discrete — программа решения обыкновенных дифференциальных уравнений, моделирование дискретного времени
• ode_root — программа решения обыкновенных дифференциальных уравнений с поиском корней
• dassl — дифференциальное алгебраическое уравнение
• impl — дифференциальное алгебраическое уравнение
• odedc — программа решения дискретно-непрерывных ОДУ
• odeoptions — установка опций для программ решения ОДУ
• csim — simulation (time response) of linear system
• ltitr — discrete time response (state space)
• rtitr — discrete time response (transfer matrix)
• intg — определённый интеграл

Литература

Alan C. Hindmarsh, "lsode and lsodi, two new initial value ordinary differential equation solvers", ACM-Signum newsletter, vol. 15, no. 4 (1980), pp. 10-11.

Используемые функции

Связанные процедуры могут быть найдены в директории SCI/modules/differential_equations/src/fortran: lsode.f lsoda.f lsodar.f