Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
fft
fast Fourier transform.
ifft
fast Fourier transform.
Calling Sequence
X=fft(A [,sign] [,option]) X=fft(A,sign,selection [,option]) X=fft(A,sign,dims,incr [,option] )
Arguments
- A
a real or complex vector or real or complex array (vector, matrix or N-D array.
- X
- a real or complex array with same shape as
A. - sign
- an integer. with possible values
1or-1. Select direct or inverse transform. The default value is-1(direct transform). - option
- a character string. with possible values
"symmetric"or"nonsymmetric". Indicates ifAis symmetric or not. If this argument is omitted the algorithm automatically determines ifAis symmetric or not. See the Description part for details. - selection
- a vector containing index on
Aarray dimensions. See the Description part for details. - dims
- a vector of positive numbers with integer values, or a
vector of positive integers. See the Description part for details.
Each element must be a divisor of the total number of elements of
A.The product of the elements must be less than the total number of elements of
A. - incr
- a vector of positive numbers with integer values, or a
vector of positive integers. See the Description part for
details.
incrmust have the same number of elements thandims.Each element must be a divisor of the total number of elements of
A.The
increlements must be in strictly increasing order.
Description
This function realizes direct or inverse 1-D or N-D Discrete Fourier Transforms.- Short syntax
- direct
X=fft(A,-1 [,option])orX=fft(A [,option])gives a direct transform.- single variate
If
Ais a vector a single variate direct FFT is computed that is: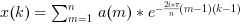
(the
-1argument refers to the sign of the exponent..., NOT to "inverse"),- multivariate
If
Ais a matrix or a multidimensional array a multivariate direct FFT is performed.
- inverse
X=fft(A,1)orX=ifft(A)performs the inverse normalized transform, such thatA==ifft(fft(A)).- single variate
- If
Ais a vector a single variate inverse FFT is computed
- multivariate
If
ais a matrix or or a multidimensional array a multivariate inverse FFT is performed.
- Long syntax for FFT along specified dimensions
X=fft(A,sign,selection [,option])allows to perform efficiently all direct or inverse fft of the "slices" ofAalong selected dimensions.For example, if
Ais a 3-D arrayX=fft(A,-1,2)is equivalent to:and
X=fft(A,-1,[1 3])is equivalent to:X=fft(A,sign,dims,incr [,option])is a previous syntax that also allows to perform all direct or inverse fft of the slices ofAalong selected dimensions.For example, if
Ais an array withn1*n2*n3elementsX=fft(A,-1,n1,1)is equivalent toX=fft(matrix(A,[n1,n2,n3]),-1,1). andX=fft(A,-1,[n1 n3],[1 n1*n2])is equivalent toX=fft(matrix(A,[n1,n2,n3]),-1,[1,3]).
- Using option argument This argument can be used
to inform the fft algorithm about the symmetry of
Aor of all its "slices". An N-D arrayBwith dimensionsn1, ...,npis conjugate symmetric for the fft if and only ifB==conj(B([1 n1:-1:2],[1 n2:-1:2],...,[1 np:-1:2])).In such a case the resultXis real and an efficient specific algorithm can be used. - "symmetric" that value causes fft to treat
Aor all its "slices" conjugate symmetric. This option is useful to avoid automatic determination of symmetry or ifAor all its "slices" are not exactly symmetric because of round-off errors. - "nonsymmetric" that value causes fft not to take care of symmetry. This option is useful to avoid automatic determination of symmetry.
- unspecified If the option is omitted the fft algorithm automatically checks for exact symmetry.
- "symmetric" that value causes fft to treat
- Optimizing fft
Remark: fftw function automatically stores his last parameters in memory to re-use it in a second time. This improves greatly the time computation when consecutives calls (with same parameters) are performed.
It is possible to go further in fft optimization using get_fftw_wisdom, set_fftw_wisdom functions.
Algorithms
This function uses the fftw3 library.
Examples
1-D fft
//Frequency components of a signal //---------------------------------- // build a noised signal sampled at 1000hz containing pure frequencies // at 50 and 70 Hz sample_rate=1000; t = 0:1/sample_rate:0.6; N=size(t,'*'); //number of samples s=sin(2*%pi*50*t)+sin(2*%pi*70*t+%pi/4)+grand(1,N,'nor',0,1); y=fft(s); //s is real so the fft response is conjugate symmetric and we retain only the first N/2 points f=sample_rate*(0:(N/2))/N; //associated frequency vector n=size(f,'*') clf() plot(f,abs(y(1:n)))
2-D fft
---------------------------------- A = zeros(256,256); A(5:24,13:17) = 1; X = fftshift(fft(A)); set(gcf(),"color_map",jetcolormap(128)); clf;grayplot(0:255,0:255,abs(X)')
mupliple fft
//simple case, 3 1-D fft at a time N=2048; t=linspace(0,10,2048); A=[2*sin(2*%pi*3*t)+ sin(2*%pi*3.5*t) 10*sin(2*%pi*8*t) sin(2*%pi*0.5*t)+4*sin(2*%pi*0.8*t)]; X=fft(A,-1,2); fs=1/(t(2)-t(1)); f=fs*(0:(N/2))/N; //associated frequency vector clf;plot(f(1:100)',abs(X(:,1:100))') legend(["3 and 3.5 Hz","8 Hz","0.5 and 0.8 Hz"],"in_upper_left") // 45 3-D fft at a time Dims=[5 4 9 5 6]; A=matrix(rand(1,prod(Dims)),Dims); y=fft(A,-1,[2 4 5]); //equivalent (but less efficient code) y1=zeros(A); for i1=1:Dims(1) for i3=1:Dims(3) ind=list(i1,:,i3,:,:); y1(ind(:))=fft(A(ind(:)),-1); end end
//Using explicit formula for 1-D discrete Fourier transform //------------------------------------------------ function xf=DFT(x, flag); n=size(x,'*'); //Compute the n by n Fourier matrix if flag==1 then,//backward transformation am=exp(2*%pi*%i*(0:n-1)'*(0:n-1)/n); else //forward transformation am=exp(-2*%pi*%i*(0:n-1)'*(0:n-1)/n); end xf=am*matrix(x,n,1);//dft xf=matrix(xf,size(x));//reshape if flag==1 then,xf=xf/n;end endfunction //Comparison with the fast Fourier algorithm a=rand(1,1000); norm(DFT(a,1) - fft(a,1)) norm(DFT(a,-1) - fft(a,-1)) timer();DFT(a,-1);timer() timer();fft(a,-1);timer()
See Also
- corr — correlation, covariance
- fftw_flags — set method for fft planner algorithm selection
- get_fftw_wisdom — return fftw wisdom
- set_fftw_wisdom — set fftw wisdom
- fftw_forget_wisdom — Reset fftw wisdom
Bibliography
Matteo Frigo and Steven G. Johnson, "FFTW Documentation" http://www.fftw.org/#documentation
| Report an issue | ||
| << dst | transforms | hank >> |