Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
legendre
随伴ルジャンドル関数
呼び出し手順
y = legendre(n,m,x [,normflag])
パラメータ
- n
非負の整数または等間隔で増分刻みが1の 非負の整数のベクトル
- m
非負の整数または等間隔で増分刻みが1の 非負の整数のベクトル
- x
実数 (行) ベクトル (
xの要素は(-1,1)の範囲にある必要があります)- normflag
(オプション) スカラー文字列
説明
n および m がスカラーの場合,
legendre(n,m,x) は,
xの全要素について
随伴ルジャンドル関数Pnm(x)を計算します.
使用される定義を以下に示します:
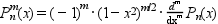
ただし,Pnはn次の
ルジャンドル多項式です.
legendre(n,0,x) は
xの全要素について
ルジャンドル関数Pn(x)を計算します.
normflagが"norm"に等しい時,
((-1)^m係数を付けずに)
正規化された出力が得られます :
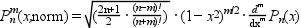
これは,球面調和関数を計算する際に有用です(例3参照):
効率化のため,
最初の2つの引数の一つをベクトルとすることができ,
例えば,legendre(n1:n2,0,x)は
xの要素における
n1, n1+1, ..., n2次の
ルジャンドル多項式を全て計算します.
また,
legendre(n,m1:m2,x) は
xにおいてm=m1, m1+1, ..., m2
に関する随伴ルジャンドル関数Pnmを全て計算します.
出力形式
どの場合でも, yの形式は以下のようになります :
and :
y(i,j) = P(n(i),m;x(j)) n がベクトルの場合 y(i,j) = P(n,m(i);x(j)) m がベクトルの場合 y(1,j) = P(n,m;x(j)) n と m が共にスカラーの場合
xは行ベクトルの方が好ましいですが,
任意のmx x nx行列を指定すると,
1 x (mx * nx)行列とみなされ,
以下のように列順に成形されます.
例
// 例 1 : 最初の6個のルジャンドル多項式を(-1,1)の範囲でプロット l = nearfloat("pred",1); x = linspace(-l,l,200)'; y = legendre(0:5, 0, x); clf() plot2d(x,y', leg="p0@p1@p2@p3@p4@p5@p6") xtitle("the 6 th first Legendre polynomials") // 例2 : 5次の随伴ルジャンドル関数をプロット l = nearfloat("pred",1); x = linspace(-l,l,200)'; y = legendre(5, 0:5, x, "norm"); clf() plot2d(x,y', leg="p5,0@p5,1@p5,2@p5,3@p5,4@p5,5") xtitle("the (normalised) associated Legendre functions of degree 5") // 例3 : 球面調和関数を定義,プロット // 3-1 : 関数Ylmを定義 function [y]=Y(l, m, theta, phi) // theta はスカラーまたは行ベクトル // phi はスカラーまたは列ベクトル if m >= 0 then y = (-1)^m/(sqrt(2*%pi))*exp(%i*m*phi)*legendre(l, m, cos(theta), "norm") else y = 1/(sqrt(2*%pi))*exp(%i*m*phi)*legendre(l, -m, cos(theta), "norm") end endfunction // 3.2 : 他の有用な関数を定義 function [x, y, z]=sph2cart(theta, phi, r) // theta 行ベクトル 1 x nt // phi 列ベクトル np x 1 // r スカラーまたは np x nt 行列 (r(i,j) phi(i) theta(j)) における長さ x = r.*(cos(phi)*sin(theta)); y = r.*(sin(phi)*sin(theta)); z = r.*(ones(phi)*cos(theta)); endfunction // 3-3 Y31(theta,phi)をプロット l = 3; m = 1; theta = linspace(0.1,%pi-0.1,60); phi = linspace(0,2*%pi,120)'; f = Y(l,m,theta,phi); [x1,y1,z1] = sph2cart(theta,phi,abs(f)); [xf1,yf1,zf1] = nf3d(x1,y1,z1); [x2,y2,z2] = sph2cart(theta,phi,abs(real(f))); [xf2,yf2,zf2] = nf3d(x2,y2,z2); [x3,y3,z3] = sph2cart(theta,phi,abs(imag(f))); [xf3,yf3,zf3] = nf3d(x3,y3,z3); clf() subplot(1,3,1) plot3d(xf1,yf1,zf1,flag=[2 4 4]); xtitle("|Y31(theta,phi)|") subplot(1,3,2) plot3d(xf2,yf2,zf2,flag=[2 4 4]); xtitle("|Real(Y31(theta,phi))|") subplot(1,3,3) plot3d(xf3,yf3,zf3,flag=[2 4 4]); xtitle("|Imag(Y31(theta,phi))|")
作者
- Smith, John M. (code dxlegf.f from Slatec)
- B. Pincon (scilab interface)
| << gammaln | Special Functions | oldbesseli >> |