Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
semidef
semidefinite programming
Calling Sequence
[x,Z,ul,info]=semidef(x0,Z0,F,blck_szs,c,options)
Arguments
- x0
m-by-1 real column vector (must be strictly primal feasible, see below)
- Z0
L-by-1 real vector (compressed form of a strictly feasible dual matrix, see below)
- F
L-by-(m+1) real matrix
- blck_szs
p-by-2 integer matrix (sizes of the blocks) defining the dimensions of the (square) diagonal blocks
size(Fi(j)=blck_szs(j) j=1,...,m+1.- c
m-by-1 real vector
- options
a 1-by-5 matrix of doubles
[nu,abstol,reltol,tv,maxiters]- ul
a 1-by-2 matrix of doubles.
Description
semidef solves the semidefinite program:
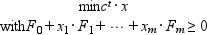
and its dual:
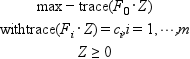
exploiting block structure in the matrices
F_i.
The Fi's matrices are stored columnwise in
F in compressed format: if F_i^j,
i=0,..,m, j=1,...,L denote the jth (symmetric) diagonal block of
F_i, then
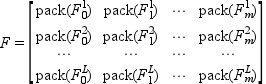
where pack(M), for symmetric
M, is the vector
[M(1,1);M(1,2);...;M(1,n);M(2,2);M(2,3);...;M(2,n);...;M(n,n)]
(obtained by scanning rowwise the upper triangular part of
M).
blck_szs gives the size of block
j, ie,
size(F_i^j)=blck_szs(j).
Z is a block diagonal matrix with L blocks Z^0, ...,
Z^{L-1}. Z^j has size blck_szs[j]
times blck_szs[j]. Every block is stored using packed storage of
the lower triangular part.
The 1-by-2 matrix of doubles ul contains the primal objective
value c'*x and the dual objective value
-trace(F_0*Z).
The entries of options are respectively:
nu: a real parameter which ntrols the rate of convergence.abstol: absolute tolerance. The absolute tolerance cannot be lower than 1.0e-8, that is, the absolute tolerance used in the algorithm is the maximum of the user-defined tolerance and the constant tolerance 1.0e-8.reltol: relative tolerance (has a special meaning when negative).tv: the target value, only referenced ifreltol < 0.maxiters: the maximum number of iterations, a positive integer value.
On output, the info variable contains the status of the execution.
info=1if maxiters exceeded,info=2if absolute accuracy is reached,info=3if relative accuracy is reached,info=4if target value is reached,info=5if target value is not achievable;negative values indicate errors.
Convergence criterion is based on the following conditions that is, the algorithm stops if one of the following conditions is true:
maxiters is exceeded
duality gap is less than abstol
primal and dual objective are both positive and duality gap is less than (
reltol* dual objective) or primal and dual objective are both negative and duality gap is less than (reltol* minus the primal objective)reltol is negative and primal objective is less than tv or dual objective is greater than
tv.
Implementation notes
This function is based on L. Vandenberghe and S. Boyd sp.c program.
Examples
F0=[2,1,0,0; 1,2,0,0; 0,0,3,1 0,0,1,3]; F1=[1,2,0,0; 2,1,0,0; 0,0,1,3; 0,0,3,1] F2=[2,2,0,0; 2,2,0,0; 0,0,3,4; 0,0,4,4]; blck_szs=[2,2]; F01=F0(1:2,1:2);F02=F0(3:4,3:4); F11=F1(1:2,1:2);F12=F1(3:4,3:4); F21=F2(1:2,1:2);F22=F2(3:4,3:4); x0=[0;0] Z0=2*F0; Z01=Z0(1:2,1:2);Z02=Z0(3:4,3:4); FF=[[F01(:);F02(:)],[F11(:);F12(:)],[F21(:);F22(:)]] ZZ0=[[Z01(:);Z02(:)]]; c=[trace(F1*Z0);trace(F2*Z0)]; options=[10,1.d-10,1.d-10,0,50]; [x,Z,ul,info]=semidef(x0,pack(ZZ0),pack(FF),blck_szs,c,options) w=vec2list(unpack(Z,blck_szs),[blck_szs;blck_szs]); Z=sysdiag(w(1),w(2)) c'*x+trace(F0*Z) spec(F0+F1*x(1)+F2*x(2)) trace(F1*Z)-c(1) trace(F2*Z)-c(2)
References
L. Vandenberghe and S. Boyd, " Semidefinite Programming," Informations Systems Laboratory, Stanford University, 1994.
Ju. E. Nesterov and M. J. Todd, "Self-Scaled Cones and Interior-Point Methods in Nonlinear Programming," Working Paper, CORE, Catholic University of Louvain, Louvain-la-Neuve, Belgium, April 1994.
SP: Software for Semidefinite Programming, http://www.ee.ucla.edu/~vandenbe/sp.html
| << recons | Optimisation et Simulation | vec2list >> |