Scilab-Branch-5.3-GIT
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
interp
3次スプライン評価関数
呼び出し手順
[yp [,yp1 [,yp2 [,yp3]]]]=interp(xp, x, y, d [, out_mode])
パラメータ
- xp
実数ベクトルまたは行列
- x,y,d
同じ大きさの実数ベクトルで, 3次スプラインまたはサブスプライン関数を定義します (以下では
sと呼ばれます)- out_mode
範囲 [x1,xn] の外側で
sの評価値を定義する (オプションの) 文字列- yp
xpと同じ大きさのベクトルまたは行列で, (xp(yp(i)=s(xp(i) または yp(i,j)=s(xp(i,j)において)sを要素毎に評価したもの)- yp1, yp2, yp3
xpと同じ大きさのベクトル(または行列)で,xp上におけるsの逐次微分の 要素毎の評価
説明
yi=s(xi), di = s'(xi)の時,
スプラインまたはサブスプライン関数(splin参照)
を定義する3つのベクトル (x,y,d)を指定すると,
この関数は,xp(i)において
s (および要すればs', s'', s''')
を評価します:
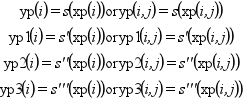
out_modeパラメータは
補外,すなわち,xp(i)が[x1,xn]の範囲にない場合
の評価規則を設定します :
- "by_zero"
0による補外が行われます
- "by_nan"
Nanによる補外
- "C0"
以下のように定義される補外 :
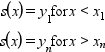
- "natural"
以下のように定義される補外 (p_i は[x_i,x_{i+1}] において
sを定義する 多項式です) :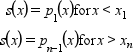
- "linear"
補外は以下のように低意義されます :
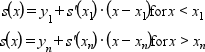
- "periodic"
sは周期性により拡張されます.
例
// splin および lsq_splinの例を参照 // スプラインおよびサブスプラインの C2およびC1連続性を示す例 a = -8; b = 8; x = linspace(a,b,20)'; y = sinc(x); dk = splin(x,y); // not_a_knot df = splin(x,y, "fast"); xx = linspace(a,b,800)'; [yyk, yy1k, yy2k] = interp(xx, x, y, dk); [yyf, yy1f, yy2f] = interp(xx, x, y, df); clf() subplot(3,1,1) plot2d(xx, [yyk yyf]) plot2d(x, y, style=-9) legends(["not_a_knot spline","fast sub-spline","interpolation points"],... [1 2 -9], "ur",%f) xtitle("spline interpolation") subplot(3,1,2) plot2d(xx, [yy1k yy1f]) legends(["not_a_knot spline","fast sub-spline"], [1 2], "ur",%f) xtitle("spline interpolation (derivatives)") subplot(3,1,3) plot2d(xx, [yy2k yy2f]) legends(["not_a_knot spline","fast sub-spline"], [1 2], "lr",%f) xtitle("spline interpolation (second derivatives)") // 異なる補外の方法を示す例 x = linspace(0,1,11)'; y = cosh(x-0.5); d = splin(x,y); xx = linspace(-0.5,1.5,401)'; yy0 = interp(xx,x,y,d,"C0"); yy1 = interp(xx,x,y,d,"linear"); yy2 = interp(xx,x,y,d,"natural"); yy3 = interp(xx,x,y,d,"periodic"); clf() plot2d(xx,[yy0 yy1 yy2 yy3],style=2:5,frameflag=2,leg="C0@linear@natural@periodic") xtitle(" different way to evaluate a spline outside its domain")
作者
B. Pincon
| << eval_cshep2d | Interpolation | interp1 >> |