- Aide Scilab
- Traitement du Signal
- How to
- fft
- Signal
- analpf
- bilt
- buttmag
- casc
- cepstrum
- cheb1mag
- cheb2mag
- chepol
- convol
- corr
- cspect
- czt
- detrend
- dft
- ell1mag
- eqfir
- eqiir
- faurre
- ffilt
- fft2
- fftshift
- filt_sinc
- filter
- find_freq
- findm
- frfit
- frmag
- fsfirlin
- group
- hank
- hilb
- hilbert
- iir
- iirgroup
- iirlp
- intdec
- jmat
- kalm
- lattn
- lattp
- lev
- levin
- lindquist
- mese
- mfft
- mrfit
- %asn
- %k
- %sn
- phc
- pspect
- remez
- remezb
- rpem
- sincd
- srfaur
- srkf
- sskf
- syredi
- system
- trans
- wfir
- wiener
- wigner
- window
- yulewalk
- zpbutt
- zpch1
- zpch2
- zpell
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
fft
Transformée de Fourier discrète rapide.
ifft
Transformée de Fourier discrète rapide inverse.
Calling Sequence
x=fft(a ,-1) ou x=fft(a) x=fft(a,1) or x=ifft(a) x=fft(a,-1,dim,incr) x=fft(a,1,dim,incr)
Arguments
- a
Vecteur ou matrice réelle ou complexe.
- x
Vecteur ou matrice réelle complexe ayant les mêmes dimensions que
a.- dim
un entier positif
- incr
un entier positif
Description
- Syntaxe courte
Si
aest un vecteur,x=fft(a,-1)oux=fft(a)calcule la transformée de Fourier discrète directe monovariable dea: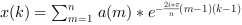
Et
x=fft(a,+1)oux=ifft(a)calcule la transformée de Fourier discrète inverse monovariable dea: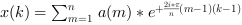
A noter: (l'argument
-1ou+1argument de la fonctionfftreprésente le signe de l'exposant de l'exponentielle.Si
aest une matrice,x=fft(a,-1)oux=fft(a)calcule la transformée de Fourier discrète directe multivariable deaEt
x=fft(a,-1)oux=fft(a)calcule la transformée de Fourier discrète inverse multivariable dea- Syntaxe longue pour la FFT mutidimensionnelle
X=fft(A,-1,dim,incr)permet de réaliser une transformée de Fourier discrète multidimensionnelle.Si
Aest un vecteur réel ou complexe implicitement indexé parj1,j2,..,jpi.e.a(j1,j2,..,jp)oùj1varie dans1:dim(1),j2dans1:dim(2),...on obtient une p-variable transformée de Fourier en appelant p fois la fonctionfftcomme suit:incrk=1; x=a; for k=1:p x=fft(x,-1,dim(k),incrk); incrk=incrk*dim(k); end
où
dimkest la dimension de la variable courante, c'est à dire celle que l'on intègre etincrkest l'incrément qui sépare deux éléments successifs indexés parjketjk+1dansa.En particulier,si
aest une matricemparnx=fft(a,-1)est équivalent aux 2 instructions:a1=fft(a,-1,m,1); x=fft(a1,-1,n,m);
Algorithme
Si le module fftw a été chargé dans Scilab
cette fonction utilise cette bibliothèque (http://www.fftw.org/). A
défaut cette fonction est basée sur les routines fortran fft842.f
(algorithme de Cooley-Tukey pour des vecteurs de taille n=2^m) et
dfftbi.f (pour les vecteurs de taille quelconque)
Examples
//Composantes fréquentielles d'un signal //---------------------------------- // Construction d'un signal bruité échantilloné à 1000hz // contenant deux fréquences pures à 50 et 70 Hz. sample_rate=1000; t = 0:1/sample_rate:0.6; N=size(t,'*'); //nombre d'échantillons s=sin(2*%pi*50*t)+sin(2*%pi*70*t+%pi/4)+grand(1,N,'nor',0,1); y=fft(s); //y est symétrique, on ne garde que N/2 points f=sample_rate*(0:(N/2))/N; //vecteur de fréquences associé n=size(f,'*') clf() plot(f,abs(y(1:n)))
//Définition directe de la transformée de Fourier discrete //-------------------------------------------------------- function xf=DFT(x, flag); n=size(x,'*'); //Calcul de la matrice de Fourier (n by n !) if flag==1 then,//transformation inverse am=exp(2*%pi*%i*(0:n-1)'*(0:n-1)/n); else //transformation directe am=exp(-2*%pi*%i*(0:n-1)'*(0:n-1)/n); end xf=am*matrix(x,n,1);//dft xf=matrix(xf,size(x));//mise en formz if flag==1 then,xf=xf/n;end endfunction //Comparaison avec l'algorithme de la transformée rapide: a=rand(1,1000); norm(DFT(a,1) - fft(a,1)) norm(DFT(a,-1) - fft(a,-1)) timer();DFT(a,-1);timer() timer();fft(a,-1);timer()
Voir aussi
| << How to | Traitement du Signal | Signal >> |