prod

product of array elements

Calling Sequence

y=prod(x)
y=prod(x,orientation)
y=prod(x,outtype)
y=prod(x,orientation,outtype)

Arguments

x

an array of reals, complex, booleans, polynomials or rational fractions.

orientation

it can be either

a string with possible values "*", "r", "c" or "m"
a number with positive integer value

outtype

a string with possible values "native" or "double".

y

scalar or array

Description

For an array x, y=prod(x) returns in the scalar y the product of all the elements of x.

y=prod(x,orientation) returns in y the product of x along the dimension given by orientation:

if orientation is equal to 1 or "r" then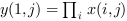

or
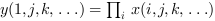
if orientation is equal to 2 or "c" then: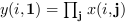

or
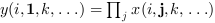
if orientation is equal to n then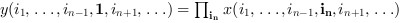
y=prod(x,"*") is equivalent to y=prod(x)
y=prod(x,"m") is equivalent to y=prod(x,orientation) where orientation is the index of the first dimension of x that is greater than 1.

The outtype argument rules the way the summation is done:

For arrays of floats, of polynomials, of rational fractions, the evaluation is always done using floating points computations. The "double" or "native" options are equivalent.
For arrays of integers,

if outtype="native" the evaluation is done using integer computations (modulo 2^b, where b is the number of bits used),

if outtype="double" the evaluation is done using floating point computations.

The default value is outtype="native".
For arrays of booleans,

if outtype="native" the evaluation is done using boolean computations ( + is replaced by |),

if outtype="double" the evaluation is done using floating point computations (%t values are replaced by 1 and %f values by 0).

The default value is outtype="double". This option is used for Matlab compatibility.

Remark

This function applies, with identical rules to sparse matrices and hypermatrices.

Examples

A=[1,2;3,4];
prod(A)
prod(A,1)

I=uint8([2 95 103;254 9 0])
prod(I) //native evaluation
prod(I,"double")
prod(I,2,"double")

s=poly(0,"s");
P=[s,%i+s;s^2,1];
prod(P),
prod(P,2)

B=[%t %t %f %f];
prod(B) //evaluation in float
prod(B,"native") //similar to or(B)