meanshift
Mean Shift clustering algorithm
Syntax
[centers, labels] = meanshift(X) [centers, labels] = meanshift(X, bandwidth) [centers, labels] = meanshift(X, bandwidth, opts)
Arguments
- X
is a N x D (N samples, D features) real matrix.
- bandwidth
a positive scalar. Radius parameter controlling the neighborhood window. Small values produce many small clusters; large values produce fewer clusters. If not provided or is equal to [], bandwidth is obtained by estimate_bandwidth.
- opts
structure with fields:
- max_iter
positive integer (default=300). Maximum number of iterations per seed for convergence.
- kernel
string (default="flat"). Kernel type for weighting points in the neighborhood. Supported values: "flat" (uniform kernel, all neighbors equally weighted) and "gaussian" (Gaussian kernel, weights decrease with distance.)
- seeds
real matrix (M x D) (default=X). Initial seed points for clustering. If not provided, seeds are initialized from the dataset.
- bin_seeding
boolean (default=%f). If %t, seeds are initialized from a grid of binned points rather than all samples, which speeds up computation on large datasets.
- min_bin_freq
positive integer (default=1). Minimum number of points required in a bin to be considered as a seed (used only when
bin_seeding=%t).
- centers
real matrix (K x D). Final cluster centers. K is the number of clusters.
- labels
integers column vector (N x 1). Cluster assignment for each point (values from 1 to K).
Description
The Mean Shift algorithm is a non-parametric clustering that draws a neighbordhood circle of
radius bandwidth around each seed, calculates the barycenter of the points
located in this circle, and moves the point towards this barycenter.
The iterations continue until the algorithm converges, that is, until the barycenters
no longer move. Two points are classified in the same class if they have converged towards
the same barycenter.
With
flatkernel, all neighbors inside the window are weighted equally.With
gaussiankernel, weights decrease smoothly with distance.
Options seeds, bin_seeding, and min_bin_freq
allow control over initialization for performance on large datasets.
Examples
Two well-separated blobs
rand("seed", 0) n = 20; X1 = [rand(n, 2) + 1; rand(n, 2) + 5]; [centers1, labels1] = meanshift(X1, 1); scf(); scatter(X1(:,1), X1(:,2), [], labels1, "fill"); plot(centers1(:,1), centers1(:,2), 'r*', "markersize", 10, "thickness", 3);
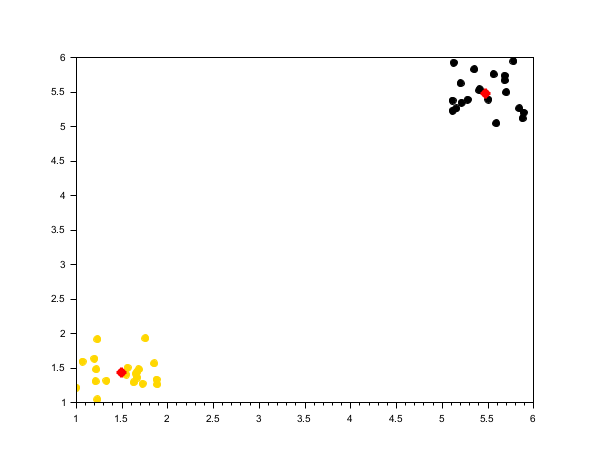
Three nearby clusters
rand("seed", 0) n = 20; X2 = [rand(n, 2) + 1; rand(n, 1) + 3, rand(n, 1) + 1; rand(n, 1) + 2, rand(n, 1) + 3]; [centers2, labels2] = meanshift(X2, 0.8); scf(); scatter(X2(:,1), X2(:,2), [], labels2, "fill"); plot(centers2(:,1), centers2(:,2), 'r*', "markersize", 10, "thickness", 3);
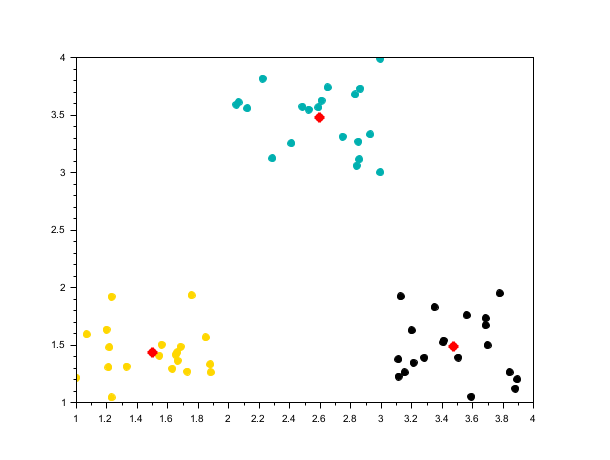
Unequal cluster sizes
rand("seed", 0) X3 = [rand(50, 2)+2; rand(5,2)+8]; opts = struct("bin_seeding", %t, "min_bin_freq", 2); [centers3, labels3] = meanshift(X3, 1.2, opts); scf(); scatter(X3(:,1), X3(:,2), [], labels3, "fill"); plot(centers3(:,1), centers3(:,2), 'r*', "markersize", 10, "thickness", 3);
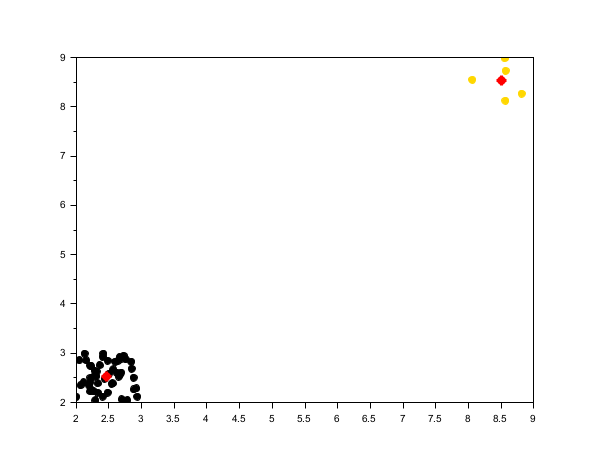
Gaussian kernel
rand("seed", 0) n = 20; X4 = [rand(n, 2) + 1; rand(n, 1) + 3 rand(n, 1) + 1]; // estimate bandwidth from data bw = estimate_bandwidth(X4, 0.3); opts = struct("kernel", "gaussian"); [centers4, labels4] = meanshift(X4, bw, opts); scf(); scatter(X4(:,1), X4(:,2), [], labels4, "fill"); plot(centers4(:,1), centers4(:,2), 'r*', "markersize", 10, "thickness", 3);
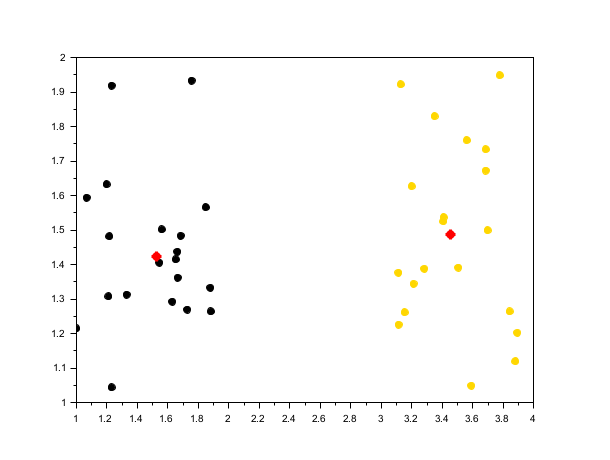
See also
- kmeans — K-means clustering
- estimate_bandwidth — Estimate an appropriate bandwidth for Mean Shift clustering
History
| Versão | Descrição |
| 2026.0.0 | Function added. |
| Report an issue | ||
| << kmeans | Estatística | polyfit >> |