dbscan
Density-based clustering (DBSCAN)
Syntax
labels = dbscan(X, eps, min_samples) [labels, core_idx] = dbscan(X, eps, min_samples)
Arguments
- X
is a N x D (N samples, D features) real matrix.
- eps
a positive scalar (default=0.5). It is the neighborhood radius. Points within distance
epsare considered neighbors.- min_samples
an integer (default=5). It is the minimum number of points required within the
epsneighborhood for a point to be considered a core point.- labels
integers column vector (N x 1). Cluster assignment for each point. The value
-1indicates a noise point.- core_idx
vector containing the indices of the core points.
Description
The DBSCAN (Density-Based Spatial Clustering of Applications with Noise) algorithm groups
points that are close to each other into clusters, based on local density. Points that are too far from others
are considered noise.
It is based on two main concepts:
eps: this is the maximum distance between two points so that they are considered in the same neighborhood.min_samplescorresponds to the minimum number of points needed to form a dense cluster.
So, each cluster is formed around core points, which are points that
have at least min_samples neighbors within distance eps.
Points close to core points but not dense enough themselves are called
border points. All remaining points are labeled as noise.
Unlike kmeans, the DBSCAN algorithm does not require the number of clusters to be specified in advance, and it can detect clusters of arbitrary shapes.
Examples
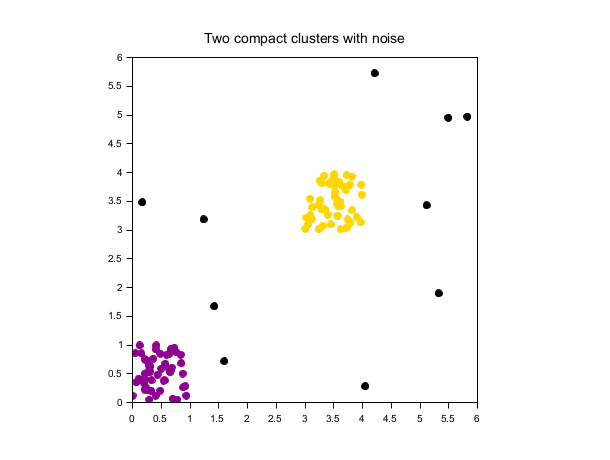
Two compact clusters with noise
rand("seed", 0) n = 50; X = [rand(n,2); rand(n,2)+3]; X = [X; 6*rand(10,2)]; labels = dbscan(X, 0.5, 5); scf(); gca().isoview = "on"; scatter(X(:,1), X(:,2), [], labels, "fill"); xtitle("Two compact clusters with noise");
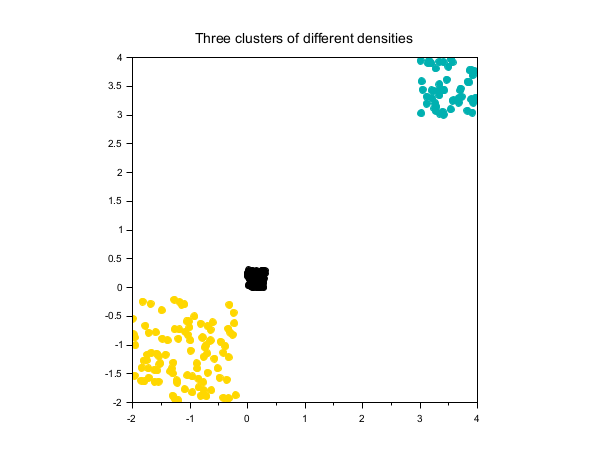
Three clusters of different densities
rand("seed", 0) X1 = 0.3*rand(100,2); X2 = rand(50,2) + 3; X3 = 1.8*rand(100,2) - 2; X = [X1; X2; X3]; labels = dbscan(X, 0.4, 5); scf(); scatter(X(:,1), X(:,2), [], labels, "fill"); xtitle("Three clusters of different densities"); gca().isoview = "on";
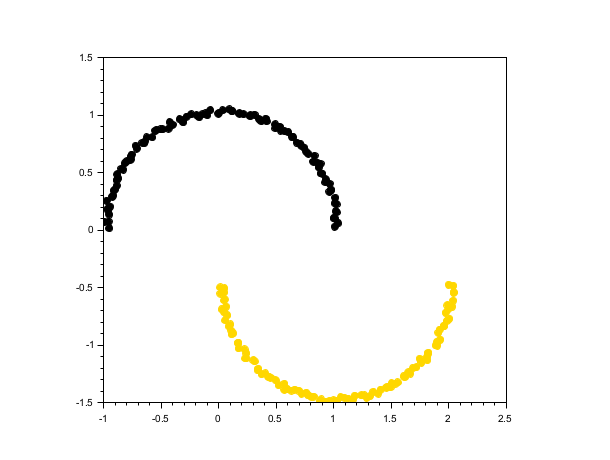
half-moon shaped data
rand("seed", 0) n = 100; t = linspace(0, %pi, n)'; X1 = [cos(t), sin(t)] + 0.05*rand(n,2); X2 = [1-cos(t), -sin(t)-0.5] + 0.05*rand(n,2); X = [X1; X2]; labels = dbscan(X, 0.2, 5); scf(); gca().isoview = "on"; scatter(X(:,1), X(:,2), [], labels, "fill");
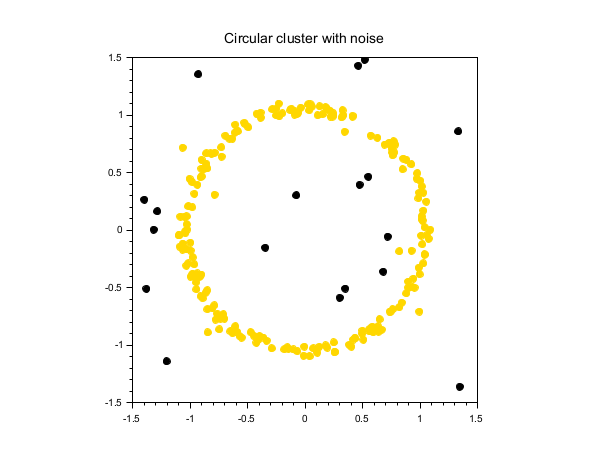
Circular cluster with noise
rand("seed", 0) theta = 2*%pi*rand(200,1); r = 1 + 0.1*rand(200,1); X1 = [r.*cos(theta), r.*sin(theta)]; // circle X2 = 3*(rand(30,2)-0.5); // noise X = [X1; X2]; labels = dbscan(X, 0.2, 5); scf(); gca().isoview = "on"; scatter(X(:,1), X(:,2), [], labels, "fill"); xtitle("Circular cluster with noise");
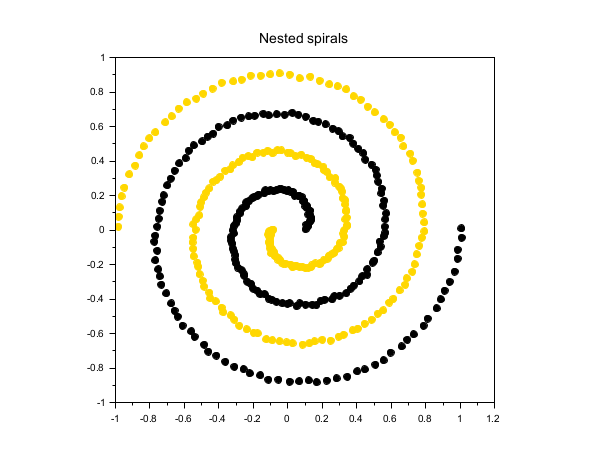
Nested spirals
rand("seed", 0) t = linspace(0, 4*%pi, 200)'; r = linspace(0.1, 1, 200)'; X1 = [r.*cos(t), r.*sin(t)] + 0.02*rand(200,2); X2 = [r.*cos(t+%pi), r.*sin(t+%pi)] + 0.02*rand(200,2); X = [X1; X2]; labels = dbscan(X, 0.15, 5); scf(); gca().isoview = "on"; scatter(X(:,1), X(:,2), [], labels, "fill"); xtitle("Nested spirals");
History
| Versão | Descrição |
| 2026.0.0 | Function added. |
| Report an issue | ||
| << Hypothesis Testing | Estatística | estimate_bandwidth >> |