arl2
SISO model realization by L2 transfer approximation
Syntax
h = arl2(y, den0, n) h = arl2(y, den0, n, imp) h = arl2(y, den0, n, imp, 'all') h = arl2(y, den0, n, 'all') [den, num, err] = arl2(..)
Arguments
- y
real vector or polynomial in
z^-1, it contains the coefficients of the Fourier's series of the rational system to approximate (the impulse response)- den0
a polynomial which gives an initial guess of the solution, it may be
poly(1,'z','c')- n
integer, the degree of approximating transfer function (degree of den)
- imp
integer in
(0,1,2)(verbose mode)- h
transfer function
num/denor transfer matrix (column vector) when flag'all'is given.- den
polynomial or vector of polynomials, contains the denominator(s) of the solution(s)
- num
polynomial or vector of polynomials, contains the numerator(s) of the solution(s)
- err
real constant or vector , the l2-error achieved for each solutions
Description
[den,num,err]=arl2(y,den0,n [,imp]) finds a pair of polynomials
num and den such that the transfer function num/den
is stable and its impulse response approximates (with a minimal l2
norm) the vector y assumed to be completed by an infinite number
of zeros.
If y(z) = y(1)(1/z)+y(2)(1/z^2)+ ...+ y(ny)(1/z^ny)
then l2-norm of num/den - y(z) is err.
n is the degree of the polynomial den.
The num/den transfer function is a L2 approximant of the
Fourier's series of the rational system.
Various intermediate results are printed according to imp.
[den,num,err]=arl2(y,den0,n [,imp],'all') returns in the
vectors of polynomials num and den a set of local
optimums for the problem. The solutions are sorted with increasing
errors err. In this case den0 is already assumed to be
poly(1,'z','c')
Examples
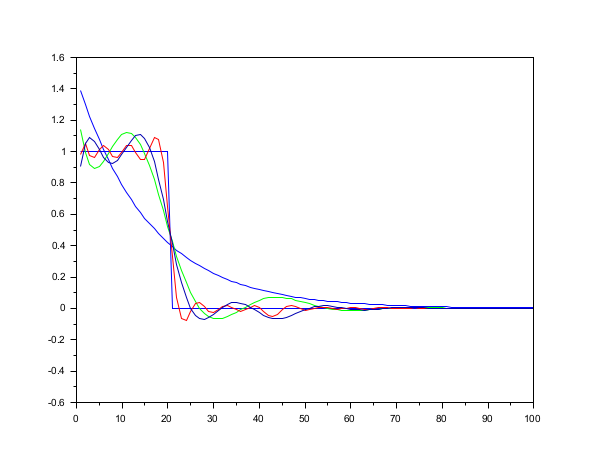
v = ones(1,20); clf(); plot2d([], [v';zeros(80,1)], 2, '051',' ',[1,-0.5,100,1.5]) [d,n,e] = arl2(v, poly(1,'z','c'),1) plot2d([], ldiv(n,d,100), 2, '000') [d,n,e] = arl2(v,d,3) plot2d([], ldiv(n,d,100), 3, '000') [d,n,e] = arl2(v,d,8) plot2d([], ldiv(n,d,100), 5, '000') [d,n,e] = arl2(v,poly(1,'z','c'),4,'all') plot2d([], ldiv(n(1),d(1),100), 10, '000')
See also
| Report an issue | ||
| << Identification | Identification | armax >> |