splin2d
interpolação por spline bicúbico em grides 2d
Seqüência de Chamamento
C = splin2d(x, y, z) C = splin2d(x, y, z, spline_type)
Parâmetros
- x,y
vetores linhas estritamente crescentes (com pelo menos dois componentes) definindo o grid de interpolação
- z
nmatriz nx x ny (nx sendo o comprimento de
xe ny o comprimento dey)- spline_type
(opcional) um string selecionando o tipo de spline bicúbico a ser computado
- C
um vetor grande com coeficientes dos elementos de área bicúbicos (veja detalhes em "Observações")
Descrição
Esta função computa um spline ou sub-spline bicúbico
s que interpola os pontos
(xi,yj,zij) i.e., temos
s(xi,yj)=zij para todo i=1,..,nx
e j=1,..,ny. O spline resultante s é definido pela
tripla (x,y,C) onde C é o vetor (com
comprimento 16(nx-1)(ny-1)) com os coeficientes de cada um dos
(nx-1)(ny-1) elementos de área bicúbicos : em [x(i)
x(i+1)]x[y(j) y(j+1)]
,s é definido por
:
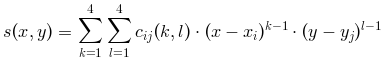
A avaliação de s em alguns pontos deve ser feita pela função
interp2d Vários tipos de splines podem ser
computados selecionando o parâmetro spline_type
apropriado. O método usada para computar os splines (ou sub-spline)
bicúbicos é o mesmo do antigo, i.e., computar em cada ponto do grid
(xi,yj) uma aproximação das derivadas primeiras
ds/dx(xi,yj) e ds/dy(xi,yj) e
das derivadas cruzadas d2s/dxdy(xi,yj). Estas
derivadas são computadas pelo modo dos esquemas do spline 1d levando a uma
função de classe C2 (s é duas vezes continuamente diferenciável) ou
através de um esquema de aproximação local, levando a uma função de classe
C1 apenas. Este esquema é selecionado através do parâmetro
spline_type (ver splin
para detalhes) :
- "not_a_knot"
é o caso padrão
- "periodic"
usado se a função subjacente é periódica: deve-se ter z(1,j) = z(nx,j) para todo j em [1,ny] e z(i,1) = z(i,ny) para i em [1,nx] #mas isto não é verificado pela interface.
Observações
De um ponto de vista de precisão, use essencialmente o tipo not_a_knot ou periodic se a função interpolada subjacente é periódica.
Os tipos natural, monotone, fast (ou fast_periodic) podem ser úteis em alguns casos, por exemplo para limitar oscilações (monotone é o mais poderoso para isso).
Para obter coeficientes dos remendos bicúbicos de um modo mais
amigável você pode usar c = matrix(C, [4,4,nx-1,ny-1])
então o coeficiente (k,l) do remendo
(i,j) (ver equação aqui antes) é armazenado em
c(k,l,i,j). Não obstante, a função interp2d espera pelo vetor grande
C e não pela hipermatriz c (note que
se pode recuperar facilmente C de c
com C=c(:)).
Exemplos
// exemplo 1 : interpolação de cos(x)cos(y) n = 7; // um grid regular com n x n pontos de interpolação // será usado x = linspace(0,2*%pi,n); y = x; z = cos(x')*cos(y); C = splin2d(x, y, z, "periodic"); m = 50; // parâmetro de discretização do grid de avaliação xx = linspace(0,2*%pi,m); yy = xx; [XX,YY] = ndgrid(xx,yy); zz = interp2d(XX,YY, x, y, C); emax = max(abs(zz - cos(xx')*cos(yy))); clf() plot3d(xx, yy, zz, flag=[2 4 4]) [X,Y] = ndgrid(x,y); param3d1(X,Y,list(z,-9*ones(1,n)), flag=[0 0]) str = msprintf(" com %d x %d pontos de interpolação. ermax = %g",n,n,emax) xtitle("Interpolação por spline de cos(x)cos(y)"+str)
// exemplo 2 : diferentes funções de interpolação em dados aleatórios n = 6; x = linspace(0,1,n); y = x; z = rand(n,n); np = 50; xp = linspace(0,1,np); yp = xp; [XP, YP] = ndgrid(xp,yp); ZP1 = interp2d(XP, YP, x, y, splin2d(x, y, z, "not_a_knot")); ZP2 = linear_interpn(XP, YP, x, y, z); ZP3 = interp2d(XP, YP, x, y, splin2d(x, y, z, "natural")); ZP4 = interp2d(XP, YP, x, y, splin2d(x, y, z, "monotone")); gcf().color_map = jet(64); clf() subplot(2,2,1) plot3d1(xp, yp, ZP1, flag=[2 2 4]) xtitle("not_a_knot") subplot(2,2,2) plot3d1(xp, yp, ZP2, flag=[2 2 4]) xtitle("bilinear interpolation") subplot(2,2,3) plot3d1(xp, yp, ZP3, flag=[2 2 4]) xtitle("natural") subplot(2,2,4) plot3d1(xp, yp, ZP4, flag=[2 2 4]) xtitle("monotone")
// exemplo 3 : spline not_a_knot e sub-spline monotone // em uma função de degraus a = 0; b = 1; c = 0.25; d = 0.75; // criando grid de interpolação n = 11; x = linspace(a,b,n); ind = find(c <= x & x <= d); z = zeros(n,n); z(ind,ind) = 1; // um degrau dentro de um quadrado // criando grid de avaliação np = 220; xp = linspace(a,b, np); [XP, YP] = ndgrid(xp, xp); zp1 = interp2d(XP, YP, x, x, splin2d(x,x,z)); zp2 = interp2d(XP, YP, x, x, splin2d(x,x,z,"monotone")); // plot clf() gcf().color_map = jet(128); subplot(1,2,1) plot3d1(xp, xp, zp1, flag=[-2 6 4]) xtitle("spline (not_a_knot)") subplot(1,2,2) plot3d1(xp, xp, zp2, flag=[-2 6 4]) xtitle("subspline (monotone)")
Ver Também
- cshep2d — bidimensional cubic shepard (scattered) interpolation
- linear_interpn — interpolação linear n-dimensional
- interp2d — função de avaliação spline bicúbica (2d)
| Report an issue | ||
| << splin | Interpolação | splin3d >> |