splin
interpolação por spline cúbico
Seqüência de Chamamento
d = splin(x, y) d = splin(x, y, spline_type) d = splin(x, y, spline_type, der)
Parâmetros
- x
um vetor (linha ou coluna) estritamente crescente (x deve ter pelo menos dois componentes)
- y
um vetor com o mesmo formato que
x- spline_type
(opcional) um string selecionando o tipo de spline a ser computado
- der
(optional) um vetor com dois componentes, com as derivadas nas extremidades (a ser fornecido quando spline_type="clamped")
- d
vetor com o mesmo formato que
x(dié a derivada do spline emxi)
Descrição
Esta função computa o spline cúbico ou sub-spline
s que interpola os pontos
(xi,yi) i.e., temos s(xi)=yi
para todo i=1,..,n. O spline resultante s é
completamente definido pela tripla (x,y,d) onde
d é o vetor com as derivadas nos xi:
s'(xi)=di (esta forma é chamada de forma de
Hermite ou hermitiana ). A avaliação do spline em
alguns pontos deve ser feita pela função interp.
Vários tipos de splines podem ser computados selecionando o parâmetro
spline_type apropriado:
- "not_a_knot"
este é o caso padrão, o spline cúbico é computado sob as seguintes condições (considerando n pontos x1,...,xn):
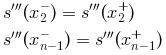
- "clamped"
neste caso, o spline cúbico é computado usando derivadas nas extremidades do intervalo que devem ser fornecidas como último argumento
der:s'(x1) = der(1) s'(xn) = der(2) - "natural"
o spline cúbico é computado sob as seguintes condições:
s''(x1) = 0 s''(xn) = 0 - "periodic"
um spline cúbico periódico é computado (
ydeve verificar y1=yn) sob as seguintes condições:s'(x1) = s'(xn) s''(x1) = s''(xn) - "monotone"
neste caso, um sub-spline (s é apenas uma vez continuamente diferenciável) é computado usando um esquema local para os di tais que s é monótono em cada intervalo:
- If y(i) ≤ y(i+1), s is increasing on
[x(i), x(i+1)]. - If y(i) ≥ y(i+1), s is increasing on
[x(i), x(i+1)].
- If y(i) ≤ y(i+1), s is increasing on
- "fast"
neste caso, um sub-spline também é computado usando um esquema local simples para os di : d(i) é a derivada em x(i) da interpolação polinomial (x(i-1),y(i-1)), (x(i),y(i)),(x(i+1),y(i+1)), exceto pelas extremidades (d1 sendo computado a partir dos 3 pontos mais à esquerda e dn dos 3 pontos mais à direita).
- "fast_periodic"
é o mesmo que o anterior, mas também usa uma fórmula centrada para d1 = s'(x1) = dn = s'(xn) através da periodicidade da função subjacente (
ydeve verificar y1=yn).
Observações
De um ponto de vista de precisão, use essencialmente o tipo
clamped se você conhece as derivadas nas
extremidades, de outro modo, use not_a_knot.
Mas se a função subjacente aproximada é periódica, use o tipo
periodic Sob boas suposições, estes tipos de spline
têm um comportamento assintótico O(h^4) do erro.
Não use o tipo natural a não ser que a função
subjacente possua zero derivadas segundas nas extremidades.
Os tipos monotone, fast
(ou fast_periodic) podem ser úteis e alguns caso, por
exemplo, para limitar oscilações (estes tipos de sub-splines têm um
comportamento assintótico O(h^3) do erro).
Se n=2 (e spline_type não é
clamped) é usada interpolação linear. Se
n=3 e spline_type é
not_a_knot, então, um sub-spline tipo
fast é computado, na verdade.
Exemplos
// exemplo 1 deff("y=runge(x)","y=1 ./(1 + x.^2)") a = -5; b = 5; n = 11; m = 400; x = linspace(a, b, n)'; y = runge(x); d = splin(x, y); xx = linspace(a, b, m)'; yyi = interp(xx, x, y, d); yye = runge(xx); clf() plot2d(xx, [yyi yye], style=[2 5], leg="interpolação por@função exata") plot2d(x, y, -9) xtitle("Intepolação da função de Runge") // exemplo 2 : mostra comportamento de splines diferentes em dados aleatórios a = 0; b = 1; // intervalo de interpolação n = 10; // número de pontos de interpolação m = 800; // discretização para avaliação x = linspace(a,b,n)'; // abscissas dos pontos de interpolação y = rand(x); // ordenadas dos pontos de interpolação xx = linspace(a,b,m)'; yk = interp(xx, x, y, splin(x,y,"not_a_knot")); yf = interp(xx, x, y, splin(x,y,"fast")); ym = interp(xx, x, y, splin(x,y,"monotone")); clf() plot2d(xx, [yf ym yk], style=[5 2 3], strf="121", ... leg="fast@monotone@spline not a knot") plot2d(x,y,-9, strf="000") // para mostrar pontos de interpolação xtitle("Vários splines e sub-splines em dados aleatórios") show_window()
Ver Também
| Report an issue | ||
| << smooth | Interpolação | splin2d >> |