corr
correlation, covariance
Syntax
[cov,Mean] = corr(x,[y],nlags) [cov,Mean] = corr('fft',xmacro,[ymacro],n,sect) [w,xu] = corr('updt',x1,[y1],w0) [w,xu] = corr('updt',x2,[y2],w,xu) ... wk = corr('updt',xk,[yk],w,xu)
Arguments
- x
a real vector
- y
a real vector, default value x.
- nlags
integer, number of correlation coefficients desired.
- xmacro
a scilab external (see below).
- ymacro
a scilab external (see below), default value xmacro
- n
an integer, total size of the sequence (see below).
- sect
size of sections of the sequence (see below).
- xi
a real vector
- yi
a real vector,default value xi.
- cov
real vector, the correlation coefficients
- Mean
real number or vector, the mean of x and if given y
Description
corr(x,y,…) computes
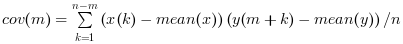 for
for m = 0, …, nlag-1.
Note that if x and y sequences are differents corr(x,y,...) is different with corr(y,x,...)
- Short sequences
[cov,Mean]=corr(x,[y],nlags)returns the first nlags correlation coefficients and Mean =mean(x)(mean of[x,y]ifyis an argument). The sequencex(resp.y) is assumed real, andxandyare of same dimension n.- Long sequences
[cov,Mean]=corr('fft',xmacro,[ymacro],n,sect). Herexmacrois eithera function of type
[xx]=xmacro(sect,istart)which returns a vectorxxof dimensionnsectcontaining the part of the sequence with indices fromistarttoistart+sect-1.a fortran subroutine or C procedure which performs the same calculation. (See the source code of
dgetxfor an example).
n= total size of the sequence.sect= size of sections of the sequence.sectmust be a power of 2.covhas dimensionsect. Calculation is performed by FFT.- Updating method
[w,xu]=corr('updt',x1,[y1],w0) [w,xu]=corr('updt',x2,[y2],w,xu) ... wk=corr('updt',xk,[yk],w,xu)
With this syntax the calculation is updated at each call to
corr.w0 = zeros(1,2*nlags); nlags = power of 2.
x1,x2,...are parts ofxsuch thatx=[x1,x2,...]and sizes ofxia power of 2. To getnlagscoefficients a final fft must be performedc=fft(w,1)/n;cov=c(1nlags)(nis the size ofx (y)). Caution: this syntax assumes thatxmean = ymean = 0.
Examples
x = %pi/10:%pi/10:102.4*%pi; rand('seed'); rand('normal'); y = [.8 * sin(x) + .8 * sin(2*x) + rand(x); .8 * sin(x) + .8 * sin(1.99*x) + rand(x)]; c = []; for j = 1:2 for k = 1:2 c = [c; corr(y(k, :), y(j, :), 64)]; end end c = matrix(c, 2, 128); cc = []; for j = 1:64 cc = [cc; c(:, (j - 1) * 2 + 1:2 * j)]; end
rand('seed'); rand('normal'); x = rand(1, 256); y = -x; deff('[z] = xx(inc, is)','z = x(is:is+inc-1)'); deff('[z] = yy(inc, is)','z = y(is:is+inc-1)'); [c, mxy] = corr(x, y, 32); x = x - mxy(1) * ones(x); y = y - mxy(2) * ones(y); //centring c1 = corr(x, y, 32); c2 = corr(x, 32); norm(c1 + c2, 1) [c3, m3] = corr('fft', xx, yy, 256, 32); norm(c1 - c3, 1) [c4, m4] = corr('fft', xx, 256, 32); norm(m3, 1) norm(m4, 1) norm(c3 - c1, 1) norm(c4 - c2, 1) x1 = x(1:128); x2 = x(129:256); y1 = y(1:128); y2 = y(129:256); w0 = zeros(1, 64); [w1, xu] = corr('u', x1, y1, w0); w2 = corr('u', x2, y2, w1, xu); zz = real(fft(w2, 1)) / 256; c5 = zz(1:32); norm(c5 - c1, 1) [w1, xu] = corr('u', x1, w0); w2 = corr('u', x2, w1, xu); zz = real(fft(w2, 1)) / 256; c6 = zz(1:32); norm(c6 - c2, 1)
// test for Fortran or C external deff('[y] = xmacro(sec, ist)','y = sin(ist:(ist+sec-1))'); x = xmacro(100, 1); [cc1, mm1] = corr(x, 2^3); [cc, mm] = corr('fft', xmacro, 100, 2^3); [cc2, mm2]=corr('fft', 'corexx', 100, 2^3); [max(abs(cc - cc1)), max(abs(mm - mm1)), max(abs(cc - cc2)), max(abs(mm - mm2))] deff('[y] = ymacro(sec, ist)','y = cos(ist:(ist+sec-1))'); y = ymacro(100, 1); [cc1, mm1] = corr(x, y, 2^3); [cc, mm] = corr('fft', xmacro, ymacro, 100, 2^3); [cc2, mm2] = corr('fft', 'corexx', 'corexy', 100, 2^3); [max(abs(cc - cc1)), max(abs(mm - mm1)), max(abs(cc - cc2)), max(abs(mm - mm2))]
See also
| Report an issue | ||
| << convol2d | Convolution - intercorrélation | hank >> |