int3d
definite 3D integral by quadrature and cubature method
Syntax
[result, err] = int3d(X, Y, Z, f) [result, err] = int3d(X, Y, Z, f, nf) [result, err] = int3d(X, Y, Z, f, nf, params) [result, err] = int3d(xmin, xmax, ymin, ymax, zmin, zmax, f) [result, err] = int3d(xmin, xmax, ymin, ymax, zmin, zmax, f, nf) [result, err] = int3d(xmin, xmax, ymin, ymax, zmin, zmax, f, nf, params)
Arguments
- X
a 4 by
Narray containing the abscissae of the vertices of theNtetrahedrons.- Y
a 4 by
Narray containing the ordinates of the vertices of theNtetrahedrons.- Z
a 4 by
Narray containing the third coordinates of the vertices of theNtetrahedrons.- xmin, xmax, ymin, ymax, zmin, zmax
real scalars defining a cuboid in the plane
- f
external (function or list or string) defining the integrand
f(xyz,nf), wherexyzis the vector of a point coordinates andnfis the number of the function to compute.- nf
the number of functions to integrate (default is 1)
- params
a real vector
[minpts, maxpts, epsabs, epsrel]. The default value is[0, 1000, 0.0, 1.d-5].- epsabs
Desired bound on the absolute error.
- epsrel
Desired bound on the relative error.
- minpts
Minimum number of function evaluations.
- maxpts
Maximum number of function evaluations. The number of function evaluations over each subregion is 43
- result
the integral value or vector of the integral values.
- err
estimates of absolute errors.
Description
The function calculates approximations of the definite integrals
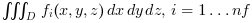 where the region of integration D is a collection of
where the region of integration D is a collection of N
tetrahedrons or the single cuboid [xmin,xmax] x [ymin,ymax] x [zmin,zmax] (which is
internally divided in 5 tetrahedrons).
A globally adaptive strategy is applied in order to compute
approximations result(k) hopefully satisfying, for each
component of I, the following claim for accuracy:
abs(I(k)-result(k))<=max(epsabs,epsrel*abs(I(k)))
int3d repeatedly subdivides the tetrahedrons with
greatest estimated errors and estimates the integrals and the errors over
the new subtetrahedrons until the error request is met or
maxpts function evaluations have been used.
A 43 point integration rule with all evaluation points inside the tetrahedron is applied. The rule has polynomial degree 8.
If the values of the input parameters epsabs or
epsrel are selected great enough, an integration rule
is applied over each tetrahedron and the results are added up to give the
approximations result(k). No further subdivision of the
tetrahedrons will then be applied.
When int3d computes estimates to a vector of
integrals, all components of the vector are given the same treatment. That
is, I(Fj) and I(Fk) for
j not equal to k, are
estimated with the same subdivision of the region of integration. For
integrals with enough similarity, we may save time by applying
int3d to all integrands in one call. For integrals that
varies continuously as functions of some parameter, the estimates produced
by int3d will also vary continuously when the same
subdivision is applied to all components. This will generally not be the
case when the different components are given separate treatment.
On the other hand this feature should be used with caution when the different components of the integrals require clearly different subdivisions.
References
Fortran routine dcutet.f
Examples
// computes the intergral of exp(x*x+y*y+z*z) over the // tetrahedron (0.,0.,0.),(1.,0.,0.),(0.,1.,0.),(0.,0.,1.) X = [0;1;0;0]; Y = [0;0;1;0]; Z = [0;0;0;1]; // function is computed by dynamically linked Fortran code [result, err] = int3d(X, Y, Z, 'int3dex') // Scilab function function v=f(xyz, numfun),v=exp(xyz'*xyz), endfunction [result, err] = int3d(X, Y, Z, f, 1, [0,100000,1.d-5,1.d-7]) // integration over a cube -1<=x<=1;-1<=y<=1;-1<=z<=1 function v=f(xyz, numfun), v=xyz'*xyz, endfunction [result, err] = int3d(-1,1,-1,1,-1,1, f, 1, [0,100000,1.d-5,1.d-7])
See also
| Report an issue | ||
| << int2d | Differential Equations | intc >> |