Scilab Website | Contribute with GitLab | Mailing list archives | ATOMS toolboxes

Scilab Online Help
2024.0.0 - Русский

Jacobian

Specifying a user-supplied Jacobian or its approximation

Syntax

... = solver( ... , jacobian = jacFn)
... = solver( ... , jacobian = jacFn, jacBand = [ml,mu])
... = solver( ... , jacBand = [ml,mu])
... = solver( ... , jacPattern = jacSp)
... = solver( ... , jacobian = jacFn, jacNonZeros = nnz, jacFormat = jFmt)

Arguments

jacFn	A Scilab function, a list, a string, a matrix (dense or sparse).
[ml,mu]	A vector of two positive integers `[mu,ml]` giving respectively the upper and lower half bandwidth of the Jacobian.
jacSp	A sparse matrix with the same sparsity pattern as the true Jacobian.
nnz	An integer, the number of non-zeros terms when the Jacobian is sparse and given as the output of a DLL entrypoint.
jFmt	A string "CSC" (the default) or "CSR" giving the sparse Jacobian format when given as the output of a DLL entrypoint.

Description

When an ODE, DAE or nonlinear equations solver method need to solve a linear system with a direct method, the Jacobian matrix of the right hand side of the system is by default approximated by finite differences. When the Jacobian is unknown but has a band structure, setting the jacBand option will allow the approximation scheme to use only mu+ml+1 calls of the right hand side, which can help the solver effort if the number of equations is large.

However, solver iterations can be accelerated and precision can be improved further by giving the true Jacobian with the jacobian option. Note that using any of the above 3 options (jacobian, jacBand, jacPattern, jacNonZeros) without specifying a method automatically selects the default one needing a Jacobian. For example specifying a Jacobian selects the BDF method in a cvode call and the inexact Newton method in a kinsol call. In addition, note that when using arkode with an implicit/explicit method jacFn denotes the Jacobian of the stiff right hand side only, which is set by the stiffRhs option (see the arkode help page). Below we consider nonlinear equations, ODEs and DAEs in three different sections as the Jacobian is defined differently, but in all situations:

the output of a Scilab function or the constant Jacobian can be a dense or a sparse matrix, and when the JacBand option is set the output must be a mu+ml+1 x n dense matrix where n is the state dimension (packed column-major banded format).
when the output of a Scilab function or the constant Jacobian is sparse, or the jacNonZeros option is set, the KLU sparse linear solver (from SuiteSparse) is selected.
when jacBand or jacPattern options are given, the Jacobian is approximated with finite differences quotients by taking into account the particular structure (band, or general sparse, respectively).
when the Jacobian is given as the output of a SUNDIALS DLL entrypoint the actual storage type of this matrix depends on the presence of the (mutualy exclusive) jacBand or jacNonZeros options, which will determine its type, respectively SUNMATRIX_BAND and SUNMATRIX_SPARSE or SUNMATRIX_DENSE by default if none of these options has been set. Hence, this is the user responsibility to use accessor macros which are compatible with the actual storage type. In the examples below we use dense Jacobians, where the matrix terms are stored using column-major order.

General information about the different ways of providing a user function (and eventual user parameters) is given in the User Functions help page.

User nonlinear equations Jacobian

In that case we deal with the Jacobian of the Nonlinear Algebraic Equations System

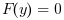
with respect to y and jacFn can be:

a Scilab function with prototype jac = jacFn(y,...), for example:

function F=fun(x)
    F = [2*x(1)-x(2)-exp(-x(1))
          -x(1)+2*x(2)-exp(-2*x(2))];
end
function J=jac(x)
    J = [2+exp(-x(1)), -1
          -1, 2+2*exp(-2*x(2))];
end
x=kinsol(fun, [0;0], jacobian=jac)

a matrix, for example for Picard iterations (here with Anderson acceleration) we give the Jacobian of the linear part of F:

function F=fun(x)
    F = [2*x(1)-x(2)-exp(-x(1))
          -x(1)+2*x(2)-exp(-2*x(2))];
end
function J=jac(x)
    J = [2, -1
        -1,  2];
end
x = kinsol(fun, [0;0], jacobian=[2 -1; -1 2], method="Picard", accel=1, display="iter")

a string giving the name of a SUNDIALS DLL entrypoint with C prototype

int sunJac(N_Vector x, N_Vector f, SUNMatrix J, 
           void *user_data, N_Vector tmp1, N_Vector tmp2)

The current value F(y) is passed by convenience as it may be used in the computation and the Jacobian has to be stored in the SUNMatrix J argument, as in the following example:

code=[
    "#include <math.h>"
    "#include <nvector/nvector_serial.h>"
    "#include <sunmatrix/sunmatrix_dense.h>"
    "int sunRhs(N_Vector X, N_Vector F, void *user_data)"    
    "{"
    "double *x = NV_DATA_S(X);"
    "double *f = NV_DATA_S(F);"
    "f[0] = 2*x[0]-x[1]-exp(-x[0]);"
    "f[1] = -x[0]+2*x[1]-exp(-2*x[0]);"
    "return 0;"
    "}"
    "int sunJac(N_Vector X, N_Vector F, SUNMatrix J,"
    "           void *user_data, N_Vector tmp1, N_Vector tmp2)"
    "{"
    "double *x = NV_DATA_S(X);"
    "double *jac = SM_DATA_D(J);"
    "jac[0] = 2+exp(-x[0]);"
    "jac[1] = -1; jac[2] = -1;"
    "jac[3] = 2+2*exp(-2*x[0]);"
    "return 0;"
    "}"];
mputl(code,"code.c")
SUN_Clink(["sunRhs","sunJac"], "code.c", load=%t);
x = kinsol("sunRhs", [0 0], jacobian = "sunJac")

User ODE Jacobian

In that case we deal with the Jacobian of the right-hand side of the ODE

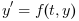
with respect to y and jacFn can be:

a Scilab function with prototype jac = jacFn(t,y,...). For example for the Van Der Pol equation:

function out=vdp1Jac(t, y)
    out = [0, 1
          -2*y(1)*y(2)-1, 1-y(1)^2];
end
[t,y] = cvode(%SUN_vdp1, [0 10], [0; 2], jacobian = vdp1Jac);

a matrix, which allows to inform the solver that a right hand side is linear.

function dydt=f(t, y, a)
    dydt=a*y;
end
function dydt=fE(t, y, a)
    dydt=-y.^3
end
A = [0 1;-1 0];
[t1,y1] = cvode(list(f,A), [0 10], [1;0], jacobian = A)
[t2,y2] = arkode(fE,[0 10],[1;0], stiffRhs=list(f,A), jacobian = A)
[t3,y3] = arkode(fE,[0 10],[1;0], stiffRhs=list(f,A), jacobian = sparse(A))

a string giving the name of a SUNDIALS DLL entrypoint with C prototype

int sunJac(realtype t, N_Vector y, N_Vector fy, SUNMatrix J, 
           void *user_data, N_Vector tmp1, N_Vector tmp2, N_Vector tmp3)

The current derivative fy=f(t,y) is passed by convenience as it may be used in the computation and the Jacobian has to be stored in the SUNMatrix J argument, as in the following example:

code=[
    "#include <nvector/nvector_serial.h>"
    "#include <sunmatrix/sunmatrix_dense.h>"
    "int sunRhs(realtype t, N_Vector Y, N_Vector Yd, void *user_data)"    
    "{"
    "double *y = NV_DATA_S(Y);"
    "double *ydot = NV_DATA_S(Yd);"
    "double *mu = (double *) user_data;"
    "ydot[0] = y[1];"
    "ydot[1] = mu[0]*(1-y[0]*y[0])*y[1]-y[0];"
    "return 0;"
    "}"
    "int sunJac(realtype t, N_Vector Y, N_Vector Yd, SUNMatrix J,"
    "           void *user_data, N_Vector tmp1, N_Vector tmp2, N_Vector tmp3)"
    "{"
    "double *y = NV_DATA_S(Y);"
    "double *jac = SM_DATA_D(J);"
    "double *mu = (double *) user_data;"
    "jac[0] = 0; jac[1] = -2.0*mu[0]*y[0]*y[1]-1.0;"
    "jac[2] = 1.0; jac[3] = mu[0]*(1.0-y[0]*y[0]);"
    "return 0;"
    "}"];
mputl(code,"code.c")
SUN_Clink(["sunRhs","sunJac"], "code.c", load=%t);
[t1,y1] = cvode(list("sunRhs",1), [0 10], [2;1], jacobian = list("sunJac", 1));

User DAE Jacobian

In that case the user function is supposed to compute

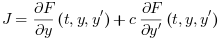
$J=\frac{\partial F}{\partial y}(t,y,y^\prime)+c\frac{\partial F}{\partial y^\prime}(t,y,y^\prime)$

where the DAE is given by 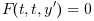$F(t,t,y^\prime)=0$ and c is an arbitrary scalar. The option value jacFn can be:

a Scilab function with prototype jac = jacFn(t,y,yp,c, ...). For example for the SIR system:

function res=sir(t, y, yp, bet, gam)
    res=[yp(1)+bet*y(1)*y(2)
         yp(2)-bet*y(1)*y(2)+gam*y(2)  
         y(1)+y(2)+y(3)-1];
end
function jac=sir_jac(t, y, yp, c, bet, gam)
    jac = [ bet*y(2)+c  bet*y(1)       0
           -bet*y(2)   -bet*y(1)+gam+c 0
            1           1              1];
end
gam=1/40;
bet=0.2;
y0=[0.999;0.001;0];
yp0 = [-bet*y0(1)*y0(2);+bet*y0(1)*y0(2)-gam*y0(2);gam*y0(2)];                        
sol = ida(list(sir,bet,gam), [0 200], y0, yp0, jacobian = list(sir_jac,bet,gam));

a cell containing the constant Jacobians with respect to y and yp:

function out=res(t, y, yp, A, B)
    out = A*yp-B*y;
end
A = [2 1; 1 1];
B = [0 1;-1 -1];
y0 = [1;0];
yp0 = A\(B*y0);
sol = ida(list(res,A,B), [0 10], y0, yp0);
solj = ida(list(res,A,B), [0 10], y0, yp0, jacobian = {-B,A});

a string giving the name of a DLL entrypoint with C prototype

int sunJacRes(realtype t, realtype cj, N_Vector Y, N_Vector Yd, N_Vector R, SUNMatrix J,
              void *user_data, N_Vector tmp1, N_Vector tmp2, N_Vector tmp3)

The current residual R is passed by convenience as it may be used in the computation. The output matrix J is the sum of the Jacobian w.r.t. y and c times the Jacobian w.r.t. y'. The Here is a full example (Robertson DAE):

code=[
    "#include <nvector/nvector_serial.h>"
    "#include <sunmatrix/sunmatrix_dense.h>"
    "int chemRes(realtype t, N_Vector Y, N_Vector Yd, N_Vector R, void *user_data)"
    "{"
    "double *y = NV_DATA_S(Y);"
    "double *yd = NV_DATA_S(Yd);"
    "double *r =  NV_DATA_S(R);"
    "r[0] = yd[0]+0.04*y[0]-1.0e4*y[1]*y[2];"
    "r[1] = yd[1]-0.04*y[0]+1.0e4*y[1]*y[2]+3.0e7*y[1]*y[1];"
    "r[2] = y[0]+y[1]+y[2]-1;"
    "return 0;"
    "}"
    "int chemJac(realtype t, realtype cj, N_Vector Y, N_Vector Yd, N_Vector R, SUNMatrix J,"
    "    void *user_data, N_Vector tmp1, N_Vector tmp2, N_Vector tmp3)"
    "{"
    "double *y = NV_DATA_S(Y);"
    "double *jac = SM_DATA_D(J);"
    "// first column"
    "jac[0] = 0.04+cj;"
    "jac[1] =  -0.04;"
    "jac[2] =  1.0;"
    "// second column"
    "jac[3] =  -1.0e4*y[2];"
    "jac[4] = +1.0e4*y[2]+2*3.0e7*y[1]+cj;"
    "jac[5] =  1.0;"
    "// third column"
    "jac[6] =  -1.0e4*y[1];"
    "jac[7] = +1.0e4*y[1];"
    "jac[8] =  1.0;"
    "return 0;"
    "}"];
mputl(code, 'code.c');
SUN_Clink(["chemRes","chemJac"], "code.c", load = %t);
y0 = [1-1e-3; 0; 1e-3];
yp0 = [-0.0400; 0.0400; 0];
tspan = [0 4e6];
[t,y] = ida("chemRes", tspan, y0, yp0, jacobian = "chemJac");
y(2,:)=y(2,:)*20000;
semilogx(t(2:$),y(:,2:$))

Report an issue
<< Events	Options, features and user functions	Options (kinsol) >>