ndgrid
construit des matrices ou hypermatrices en répliquant des vecteurs
Séquences d'appel
[X, Y] = ndgrid(x) [X, Y] = ndgrid(x,y) [X, Y, Z] = ndgrid(x,y,z) [X, Y, Z, T] = ndgrid(x,y,z,t) [X1, X2, ..., Xm] = ndgrid(x1,x2,...,xm)
Paramètres
- x, y, z, ...
vecteurs de types simples quelconques possiblement distincts (booléens, entiers encodés, décimaux, complexes, polynômes, rationnels, textes). Par défaut,
y=x.- X, Y, Z, ...
Matrices (si seulement 2 vecteurs d'entrée), ou hypermatrices, toutes de tailles identiques : size(x,"*") lignes, size(y,"*") colonnes, size(z,"*") feuilles, etc.
Par ailleurs,
Xa le type dex;Ya le type dey; etc.
Description
La première application de ndgrid consiste à
construire une grille multidimensionnelle de noeuds échantillonnant
l'espace 2D ou 3D ou N-D, à partir de 2, 3 ou N vecteurs
x, y, etc.. indiquant
l'échantillonage de chaque direction de l'espace.
Pour ce faire,
- la matrice ou l'hypermatrice
Xest construite en répliquant le vecteurxdans toutes ses colonnes ; - la matrice ou l'hypermatrice
Yest construite en répliquant le vecteurydans toutes ses lignes ; - la matrice ou l'hypermatrice
Zest construite en répliquant le vecteurzen épaisseur pour tous les points (x,y) ; etc.
--> [X, Y] = ndgrid([1 3 4], [0 2 4 6]) X = 1. 1. 1. 1. 3. 3. 3. 3. 4. 4. 4. 4. Y = 0. 2. 4. 6. 0. 2. 4. 6. 0. 2. 4. 6.
Les coordonnées du noeud node(i,j) dans l'espace 2D seront alors
simplement [x(i), y(j)] maintenant données par
[X(i,j), Y(i,j)]. De même, les coordonnées du noeud
node(i,j,k) dans une grille 3D seront
[x(i), y(j), z(k)] données par
[X(i,j,k), Y(i,j,k), Z(i,j,k)].
Ce schéma de construction par réplication peut être utilisé pour construire une grille à un nombre N quelconque de dimensions. Par ailleurs, il est indépendant de la nature des vecteurs de base répliqués et peut donc être utilisé pour tous les types de données uniformes. A titre d'exemple, considérons un ensemble d'objets ayant tous 2 attributs :
- Le premier est un nombre
n, avec 2 valeurs possibles, par exemple:n = [ 3 7 ] - Le second est une lettre, avec 6 choix possibles,
par exemple:
c = ["a" "e" "i" "o" "u" "y"]
objets :
--> [N, C] = ndgrid([3 7],["a" "e" "i" "o" "u" "y"]) C = !a e i o u y ! !a e i o u y ! N = 3. 3. 3. 3. 3. 3. 7. 7. 7. 7. 7. 7.
De là, l'objet(i,j) aura les attributs
{n(i) c(j)} que l'on pourra maintenant désigner par
{N(i,j) C(i,j)}.
Ce type de grille pourra être utilisée pour initialiser un tableau
2D de structures ayant 2 champs n et c.
Les exemples suivants montrent comment utiliser les matrices ou
hypermatrices X, Y, Z produites, pour des applications
usuelles.
Exemples
Exemple #1:
// Créons une grille de points {X,Y} x = linspace(-10,2,40); y = linspace(-5,5,40); [X,Y] = ndgrid(x,y); // x et y sont répliqués pour créer la grille // Calculons des ordonnées Z(X,Y) et traçons Z(X,Y) : Z = X - 3*X.*sin(X).*cos(Y-4) ; clf() plot3d(x,y,Z, flag=[color("green") 2 4], alpha=7, theta=60); show_window()
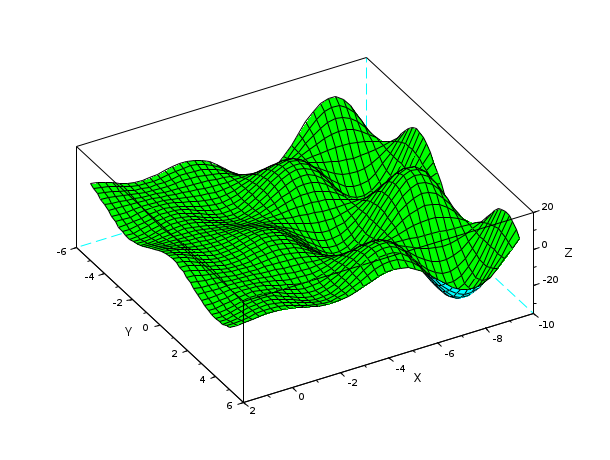
Exemple #2:
// Créons une grille en 3 dimensions nx = 10; ny = 6; nz = 4; x = linspace(0,2,nx); y = linspace(0,1,ny); z = linspace(0,0.5,nz); [X,Y,Z] = ndgrid(x,y,z); // Nous choisissons ici une représentation cartésienne, mais l'on pourrait // aussi travailler en coordonnées cylindriques, sphériques, ou autres. // Transformons les coordonnées pour plot3d() : XF=[]; YF=[]; ZF=[]; for k=1:nz [xf,yf,zf] = nf3d(X(:,:,k),Y(:,:,k),Z(:,:,k)); XF = [XF xf]; YF = [YF yf]; ZF = [ZF zf]; end for j=1:ny [xf,yf,zf] = nf3d(matrix(X(:,j,:),[nx,nz]),... matrix(Y(:,j,:),[nx,nz]),... matrix(Z(:,j,:),[nx,nz])); XF = [XF xf]; YF = [YF yf]; ZF = [ZF zf]; end // Affichage : clf() plot3d(XF,YF,ZF, flag=[0 6 3], 66, 61, leg="X@Y@Z") xtitle("A 3d grid !"); show_window()
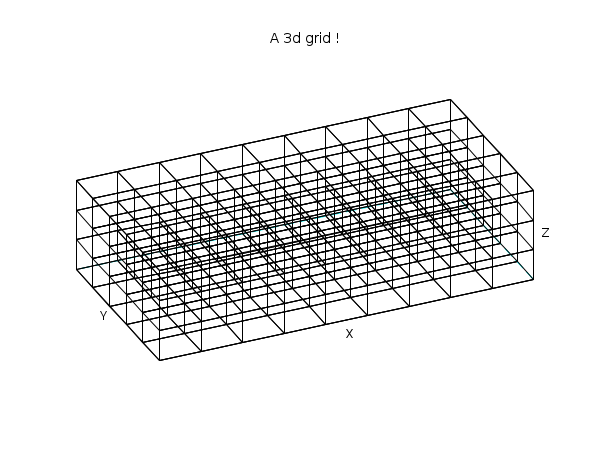
Exemple #3: création d'une table de digrammes
[c1, c2] = ndgrid(["a" "b" "c"], ["a" "b" "c" "d" "e" "f" "g" "h"]) c1+c2
--> [c1, c2] = ndgrid(["a" "b" "c"], ["a" "b" "c" "d" "e" "f" "g" "h"]) c2 = !a b c d e f g h ! !a b c d e f g h ! !a b c d e f g h ! c1 = !a a a a a a a a ! !b b b b b b b b ! !c c c c c c c c ! --> c1+c2 ans = !aa ab ac ad ae af ag ah ! !ba bb bc bd be bf bg bh ! !ca cb cc cd ce cf cg ch !
Voir aussi
Historique
| Version | Description |
| 6.0.0 | Extension à tous les types de données uniformes ([], booléens, entiers encodés, polynomes, fractions rationelles, texte). Révision de la page d'aide. |
| 6.0.1 | ndgrid(x) est désormais accepté (y=x). |
| Report an issue | ||
| << meshgrid | Matrice - génération | ones >> |