intg
definite integral
Syntax
[v, err] = intg(a, b, f) [v, err] = intg(a, b, f, atol) [v, err] = intg(a, b, f, atol, rtol) [v, err, ierr] = intg(..)
Arguments
- a, b
- Finite real numbers : bounds of the integral.
- f
- function to be integrated, specified either by its literal name (ex: "sind") or by its identifier (ex: sind), or by a list (in case of function parameters).
- atol
- real number: tolerance on the absolute error accepted on the result. Default value: 1.d-13.
- rtol
- real number: tolerance on the relative error accepted on the result. Default value: 1.d-8.
- err
- estimated absolute error on the result.
- ierr
- error flag number (= 0 if no error occurred).
Description
intg(a,b,f) evaluates the definite integral from
a to b of f(t)dt.
The function f(t) should be continuous.
The evaluation hopefully satisfies following claim for accuracy:
abs(I-v)<= max(atol, rtol*abs(I)) where
I stands for the exact value of the integral.
f is an external :
If f is function its definition must be as
follows y = f(t)
If f is a list the list must be as follows:
list(f,x1,x2,...) where f is a
function with syntax f(t,x1,x2,...).
If f is a string it refers to the name of a
Fortran function or a C procedure with a given syntax:
In the fortran case the calling sequence should be double
precision function f(x)
where x is also a
double precision number.
In the C case the syntax should be double f(double *x).
Used Functions : The associated routines dqags.f and dqagse.f from quadpack can be found in the SCI/modules/differential_equations/src/fortran directory.
Known Limitation
Like all the integrators, intg is subject to spike missing.
A flat function with a spike will be seen as a fully flat function if the spike is stiff enough.
This cannot be bypassed. It is easy to understand why when we know how the integrator operates.
Indeed, intg uses the 21-point Gauss-Kronrod rule.
Hence, any spike in-between two consecutive integration points will be undetected,
and the function will be considered smooth.
However, a warning message will be issued if the function is considered very smooth. The user will then be suggested to reduce the integration interval, should he think that spikes were missed.
The following graphs illustrate that phenomenon:
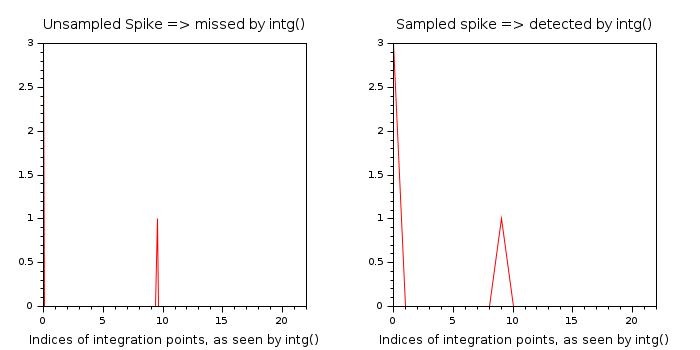
On the left image, the spike lays between the 9th and 10th integration points,
and is not detected. intg considers the function flat.
On the right, the spike is large enough to be covered by the integration points.
 | When we want to display the computed solution even if the solver has encountered an error,
we should add the third output argument ierr. Then errors become
simple warnings. This is mostly used in the case of rounding errors. |
Examples
// Function written in the Scilab language function y=f(x), y = x*sin(30*x)/sqrt(1-((x/(2*%pi))^2)), endfunction exact = -2.5432596188; I = intg(0,2*%pi,f) abs(exact-I) // Function with an argument written in the Scilab language function y=f1(x, w), y = x*sin(w*x)/sqrt(1-((x/(2*%pi))^2)), endfunction I = intg(0, 2*%pi, list(f1,30)) abs(exact - I) // Function written in Fortran (a Fortran compiler is required) // define a Fortran function cd TMPDIR; F=[' double precision function ffun(x)' ' double precision x,pi' ' pi=3.14159265358979312d+0' ' ffun=x*sin(30.0d+0*x)/sqrt(1.0d+0-(x/(2.0d+0*pi))**2)' ' return' ' end']; mputl(F,'ffun.f') // compile the function l = ilib_for_link('ffun', 'ffun.f', [], 'f'); // add the function to the working environment link(l, 'ffun', 'f') // integrate the function I = intg(0, 2*%pi, 'ffun') abs(exact - I) // Function written in C (a C compiler is required) // define a C function C=['#include <math.h>' 'double cfun(double *x)' '{' ' double y,pi=3.14159265358979312;' ' y=*x/(2.0e0*pi);' ' return *x*sin(30.0e0**x)/sqrt(1.0e0-y*y);' '}']; mputl(C, 'cfun.c') // compile the function l = ilib_for_link('cfun', 'cfun.c', [], 'c'); // add the function to the working environment link(l, 'cfun', 'c') // integrate the function I = intg(0, 2*%pi, 'cfun') abs(exact - I)
See also
History
| Version | Description |
| 6.0.2 | The default value atol of the absolute tolerance is increased from 10-14 to 10-13. |
| Report an issue | ||
| << integrate | Differential Equations | intl >> |