beta
beta function (Euler integral of the first kind)
Syntax
z = beta(x, y)
Arguments
- x, y
2 positive real scalars, vectors or matricesof equal sizes.
- z
a real or a matrix of the same size than
xwithz(i,j) = beta(x(i,j),y(i,j)).
Description
Computes the complete beta function :
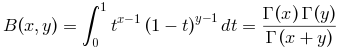
For small x and y (x+y ≤ 2 elementwise),
the algorithm uses the expression in function of the gamma function, else it
applies the exponential function onto the result of the
betaln function provided with the DCDFLIB: Library of
Fortran Routines for Cumulative Distribution Functions, Inverses, and
Other Parameter (see cdfbet for more
information about DCDFLIB).
Examples
// example 1 : beta(5,2) - beta(2,5) // symmetry (must be exactly 0) beta(0.5,0.5) // exact value is pi
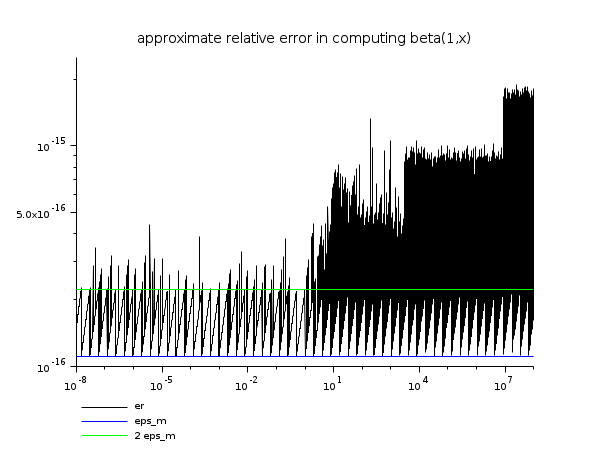
// example 2 : an error study based on the relation B(1,x) = 1/x // (computing 1/x must lead to only a relative error of eps_m, so // it may be used near as a reference to evaluate the error in B(1,x)) x = logspace(-8,8,20000)'; e = beta(ones(x),x) - (1)./x; er = abs(e) .* x; ind = find(er ~= 0); eps = ones(x(ind))*number_properties("eps"); clf() plot2d(x(ind),[er(ind) eps 2*eps],style=[1 2 3],logflag="ll",leg="er@eps_m@2 eps_m") xtitle("approximate relative error in computing beta(1,x)") show_window()
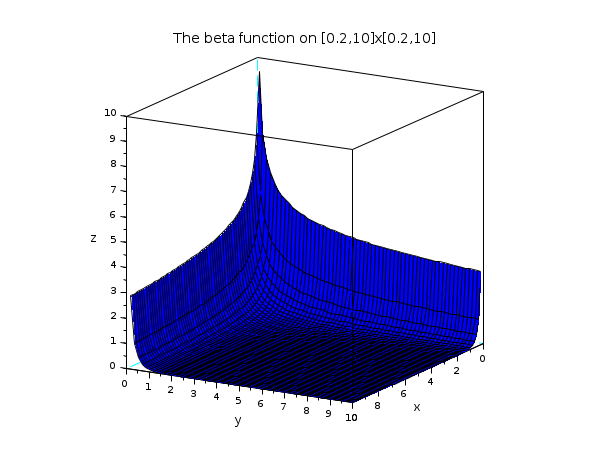
// example 3 : plotting the beta function t = linspace(0.2,10,60); X = t'*ones(t); Y = ones(t')*t; Z = beta(X,Y); clf() plot3d(t, t, Z, flag=[2 4 4], leg="x@y@z", alpha=75, theta=30) xtitle("The beta function on [0.2,10]x[0.2,10]") show_window()
See also
| Report an issue | ||
| << besseli | Special Functions | calerf >> |