lattp

引数

n

フィルタの最大次数

p

MA部の次元(定数). p= -1の場合, アルゴリズムは従来のLevinson反復を使用します.

cov

Rk(d次元過程の場合はd*d行列)を有する行列. 以下のように指定します.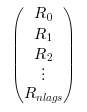

la

リスト型の変数で,連続的に計算されたAkを係数とする多項式(1次からp次)を 出力します

説明

この関数は,ARMA(n,p) プロセスのMA部を同定します.

例

//プロセス生成
t1=0:0.1:100;
y1=sin(2*%pi*t1)+sin(2*%pi*2*t1);
y1=y1+rand(y1,"normal");

//y1の共分散
nlag=128;
c1=corr(y1,nlag);
c1=c1';

//最大次数=15 および p=5 でフィルタを計算
n=5; p=2;
[la1,sig1]=lattp(n,p,c1);

参照

• levin — (多次元)LevinsonアルゴリズムによりToeplitz システムを解く
• lattn — 正規方程式の反復解