Scilab Website | Contribute with GitLab | Mailing list archives | ATOMS toolboxes

Scilab Online Help
2023.0.0 - Português

blockdiag

Creates a block diagonal matrix from provided arrays. Block diagonal system connection.

Syntax

r = blockdiag(a1,a2,...,an)

Arguments

ai

Matrices of booleans, numbers, polynomials, rationals, or strings, of any size. Sparse matrices are accepted.

subsystems (i.e. gains, or linear systems in state-space or transfer form).

r

Matrix with a1, a2, a3, ... on the diagonal. r is sparse when at least one of the ai inputs is sparse.

Description

Given the inputs A, B and C, the output will have these matrices arranged on the diagonal:

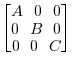
$\begin{bmatrix} A \ \ 0 \ \ 0 \\ 0 \ \ B \ \ 0 \\ 0 \ \ 0 \ \ C \end{bmatrix}$

If all the input matrices are square, the output is known as a block diagonal matrix.

If sub-systems are provided, blockdiag(..) provides the block-diagonal system made with subsystems put in the main diagonal. This can be used in particular for system interconnections.

blockdiag() can be overloaded.

Examples

With numbers:

A = [1 0 ; 0 1]
B = [3 4 5 ; 6 7 8]
C = 7
D = blockdiag(A, B, C)

--> D = blockdiag(A, B, C)
 D  =
   1.   0.   0.   0.   0.   0.
   0.   1.   0.   0.   0.   0.
   0.   0.   3.   4.   5.   0.
   0.   0.   6.   7.   8.   0.
   0.   0.   0.   0.   0.   7.

With booleans:

blockdiag([%T %T %T], [%T ; %F], [%T %F])

--> blockdiag([%T %T %T], [%T ; %F], [%T %F])
 ans  =
  T T T F F F
  F F F T F F
  F F F F F F
  F F F F T F

With polynomials:

s = %s;
blockdiag(s, [s^2 ; s^3], [1+s, 1-s^2 ; 4 s^4])

--> b = blockdiag(s, [s^2 ; s^3], [1+s, 1-s^2 ; 4 s^4])
 b  =

   s    0    0      0
         2
   0    s    0      0
         3
   0    s    0      0
                        2
   0    0    1 +s   1 -s
                     4
   0    0    4      s

With rationals:

s = %s;
blockdiag([1/s 2*s/(4*s+3)], 1/(s-1)^2)

--> blockdiag([1/s 2*s/(4*s+3)], 1/(s-1)^2)
 ans  =

   1     2s     0
   --  -------  --
   s   3 + 4s   1

   0   0            1
   --  --       -----------
                          2
   1   1        1 - 2s + s

With some sparse input:

S = blockdiag([1 2], sparse([0 3 ; 4 0]), 5)
full(S)

--> S = blockdiag([1 2], sparse([0 3 ; 4 0]), 5)
 S  =
(  4,  5) sparse matrix
(  1,  1)     1.
(  1,  2)     2.
(  2,  4)     3.
(  3,  3)     4.
(  4,  5)     5.

--> full(S)
 ans  =
   1.   2.   0.   0.   0.
   0.   0.   0.   3.   0.
   0.   0.   4.   0.   0.
   0.   0.   0.   0.   5.

With some text:

blockdiag(["Scilab" "is"],"a",["scientific" ; "software"])

--> blockdiag(["Scilab" "is"], "a", ["scientific" ; "software"])
 ans  =
!Scilab  is                 !
!            a              !
!               scientific  !
!               software    !

With mixed concatenable data types (see the page of brackets []):

blockdiag([%T %F], [-1 3], (1-%z)^2)

--> blockdiag([%T %F], [-1 3], (1-%z)^2)
 ans  =

   1    0    0    0    0

   0    0   -1    3    0
                               2
   0    0    0    0    1 -2z +z

With some linear system:

s = poly(0,'s')
blockdiag(rand(2,2), 1/(s+1), [1/(s-1);1/((s-2)*(s-3))])
blockdiag(tf2ss(1/s), 1/(s+1), [1/(s-1);1/((s-2)*(s-3))])

History

Version	Description
6.1.0	blockdiag() introduced.

Report an issue
<< random	Elementary matrices	diag >>

Copyright (c) 2022-2024 (Dassault Systèmes)
Copyright (c) 2017-2022 (ESI Group)
Copyright (c) 2011-2017 (Scilab Enterprises)
Copyright (c) 1989-2012 (INRIA)
Copyright (c) 1989-2007 (ENPC)
with contributors

Last updated:
Mon Mar 27 09:49:52 GMT 2023