interp2d
双3次スプライン (2d) 評価関数
呼び出し手順
[zp[,dzpdx,dzpdy[,d2zpdxx,d2zpdxy,d2zpdyy]]]=interp2d(xp,yp,x,y,C [,out_mode])
引数
- xp
doubleの mx行my列行列, スプラインを評価する点の
x座標.- yp
doubleの mx行my列行列, スプラインを評価する点の
y座標.- x
doubleの1行nx列行列, 補間点の
x座標値. i=1,2,...,nx-1について x(i)<x(i+1)が必要.- y
doubleの1行nx列行列, 補間点の
y座標値. i=1,2,...,nx-1について y(i)<y(i+1)が必要.- C
双3次スプラインの係数. interp2d関数の入力引数は splin2d関数の出力引数です.
- out_mode
1行1列の文字列行列, [x(1),x(nx)]x[y(1),y(ny)]の外にある値の評価
- zp
mx行my列のdouble行列, スプラインの
z座標の評価値, すなわち,i=1,2,...,mx および j = 1,2,...,my について, zp(i,j)=s(xp(i,j),yp(i,j))- dzpdx
mx行my列のdouble行列, スプラインの
xに関する1階微分.- dzpdy
mx行my列のdouble行列, スプラインの
yに関する1階微分.- d2zpdxx
mx行my列のdouble行列, スプラインの
xに関する2階微分.- d2zpdxy
mx行my列のdouble行列, スプラインの
xとyに関する2階微分.- d2zpdyy
mx行my列のdouble行列, スプラインの
yに関する2階微分.
説明
双3次スプラインまたはサブスプライン関数を定義する
3つのベクトル (x,y,C)
(splin2d参照)を指定すると,
この関数は, 次のように(xp(i),yp(i))における
s (要すれば ds/dx,
ds/dy, d2s/dxx, d2s/dxy, d2s/dyy
も)を評価します:

out_mode パラメータは,
捕外,すなわち(xp(i),yp(i))が
[x(1),x(nx)]x[y(1),y(ny)]にない場合,
の計算手法を定義します:
- "by_zero"
ゼロによる捕外が行われます
- "by_nan"
Nanによる捕外
- "C0"
捕外は以下のように定義されます :
- "natural"
捕外は(x,y)から最も近い双三次パッチにより行われます.
- "periodic"
sは周期的に拡張されます.
例
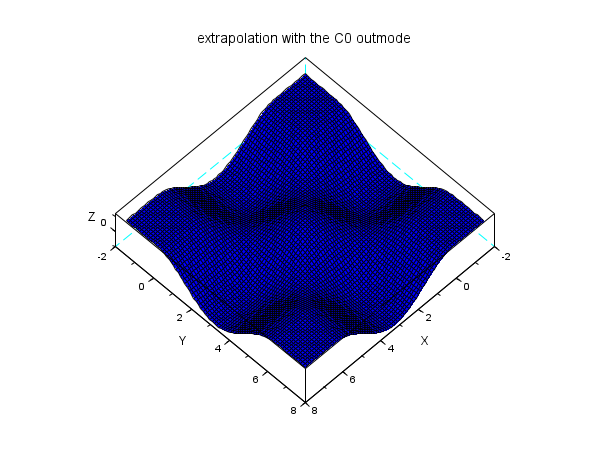
n = 7; // a n x n interpolation grid x = linspace(0,2*%pi,n); y = x; z = cos(x')*cos(y); C = splin2d(x, y, z, "periodic"); // now evaluate on a bigger domain than [0,2pi]x [0,2pi] m = 80; // discretization parameter of the evaluation grid xx = linspace(-0.5*%pi,2.5*%pi,m); yy = xx; [XX,YY] = ndgrid(xx,yy); zz1 = interp2d(XX,YY, x, y, C, "C0"); plot3d(xx, yy, zz1, flag=[2 6 4]) xtitle("extrapolation with the C0 outmode")
n = 7; // a n x n interpolation grid x = linspace(0,2*%pi,n); y = x; z = cos(x')*cos(y); C = splin2d(x, y, z, "periodic"); // now evaluate on a bigger domain than [0,2pi]x [0, m = 80; // discretization parameter of the evaluation grid xx = linspace(-0.5*%pi,2.5*%pi,m); yy = xx; [XX,YY] = ndgrid(xx,yy); zz2 = interp2d(XX,YY, x, y, C, "by_zero"); plot3d(xx, yy, zz2, flag=[2 6 4]) xtitle("extrapolation with the by_zero outmode")

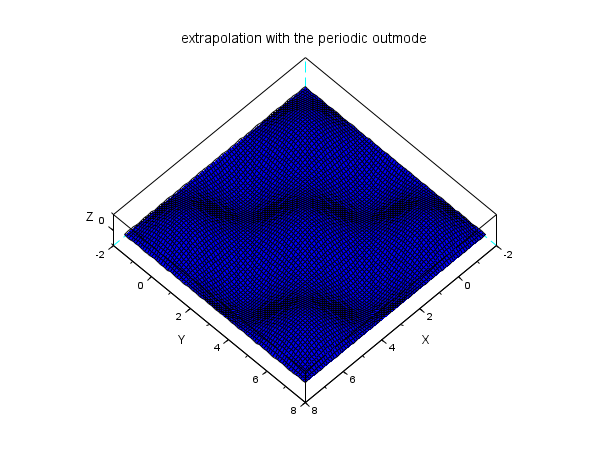
n = 7; // a n x n interpolation grid x = linspace(0,2*%pi,n); y = x; z = cos(x')*cos(y); C = splin2d(x, y, z, "periodic"); // now evaluate on a bigger domain than [0,2pi]x [0,2pi] m = 80; // discretization parameter of the evaluation grid xx = linspace(-0.5*%pi,2.5*%pi,m); yy = xx; [XX,YY] = ndgrid(xx,yy); zz3 = interp2d(XX,YY, x, y, C, "periodic"); plot3d(xx, yy, zz3, flag=[2 6 4]) xtitle("extrapolation with the periodic outmode")
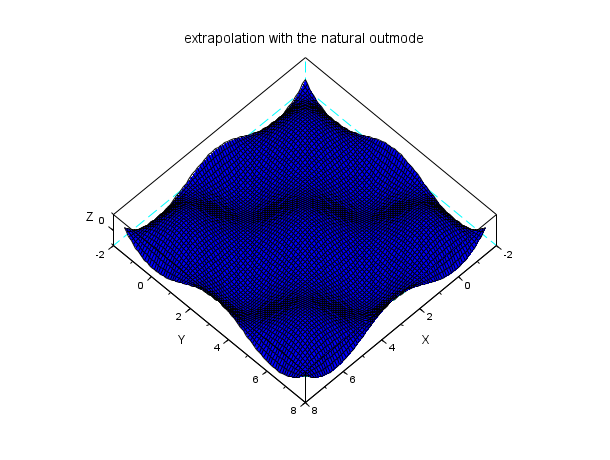
n = 7; // a n x n interpolation grid x = linspace(0,2*%pi,n); y = x; z = cos(x')*cos(y); C = splin2d(x, y, z, "periodic"); // now evaluate on a bigger domain than [0,2pi]x [0,2pi] m = 80; // discretization parameter of the evaluation grid xx = linspace(-0.5*%pi,2.5*%pi,m); yy = xx; [XX,YY] = ndgrid(xx,yy); zz4 = interp2d(XX,YY, x, y, C, "natural"); plot3d(xx, yy, zz4, flag=[2 6 4]) xtitle("extrapolation with the natural outmode")
参照
- splin2d — 双3次スプラインのグリッド2次元補間
履歴
| バージョン | 記述 |
| 5.4.0 | 以前では, 入力引数の虚部は暗黙のうちに無視されていました. |
| Report an issue | ||
| << interp1 | Interpolation | interp3d >> |