lft

Arguments

P

linear system (in state space or transfer function representation) or a simple gain, the ``augmented'' plant, implicitly partitioned into four blocks (two input ports and two output ports).

p

1x2 row vector, the dimensions of the P_22 block (see below).

R

llinear system (in state space or transfer function representation) or a simple gain, implicitly partitioned into four blocks (two input ports and two output ports).

r

1x2 row vector, dimension of the R_22 block . This argument should not be used. It is retained for compatibility with previous versions.

S

linear system, the linear fractional transform.

s

1x2 row vector, dimension of the S_22 block (see below).

Description

Linear fractional transform between two standard plants in state space form or in transfer form:

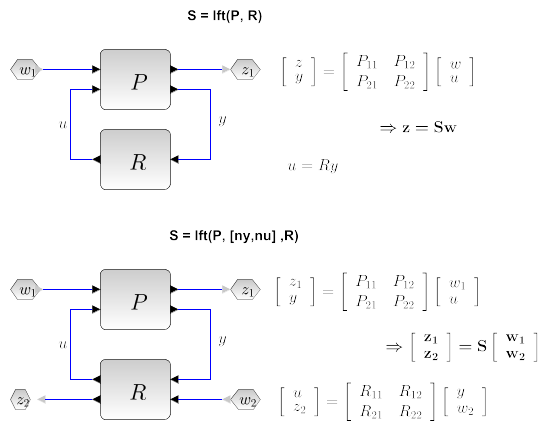
Syntax S=lft(P,R)

Computes the linear fractional transform between the systems P and a controller R. The system S corresponds to the transfer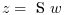

if ny and nu are respectively the number of inputs and outputs of R, one must have size(P)>=[ny nu]. The system returned is formally equivalent to

i1 = 1:($-ny);j1=1:($-nu);
i2 = ($-ny+1):$;j1=($-nu+1):$;
S = P(i1,j1) + P(i1,j2) * R * (eye() - P(i2,j2) * R) \P(i2,j1)

Using lft instead of the code above avoids numerical problems and non minimal realization.

Syntax [S,s]=lft(P,p,R)

with p= [ny,nu] Forms the generalized (2 ports) lft of P and R.

S is the two-port interconnected plant, which correspond to the transfer:

s is the dimension of the 22 block of S.

P and R can be PSSDs i.e. may admit a polynomial D matrix.

Examples

//simple feeback case

P=[1/%s, 1/(%s+1); 1/(%s+2),2/%s];
R= 1/(%s-1);
lft(P,R)

P(1,1)+P(1,2)*R*inv(1-P(2,2)*R)*P(2,1)   //Numerically dangerous!

lft(P,-1)

//Improper systems
W=[1,1;1,1/(%s^2+0.1*%s)];
K=tf2ss(1+1/%s+%s);////Improper (PID control)
lft(W,[1,1],K)

References

See also

• sensi — sensitivity functions
• augment — augmented plant
• feedback — feedback operation
• blockdiag — Creates a block diagonal matrix from provided arrays. Block diagonal system connection.