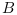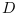Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
lqe
linear quadratic estimator (Kalman Filter)
Syntax
[K,X]=lqe(Pw)
[K,X]=lqe(P,Qww,Rvv [,Swv])
Arguments
- Pw
A state space representation of a linear dynamical system (see syslin)
- P
A state space representation of a linear dynamical system (
nuinputs,nyoutputs,nxstates) (see syslin)- Qww
Real
nxbynxsymmetric matrix, the process noise variance- Rvv
full rank real
nybynysymmetric matrix, the measurement noise variance.- Swv
real
nxbynymatrix, the process noise vs measurement noise covariance. The default value is zeros(nx,ny).- K
a real matrix, the optimal gain.
- X
a real symmetric matrix, the stabilizing solution of the Riccati equation.
Description
This function computes the linear optimal LQ estimator gain of the state estimator for a detectable (see dt_ility) linear dynamical system and the variance matrices for the process and the measurement noises.
Syntax [K,X]=lqe(P,Qww,Rvv [,Swv])
Computes the linear optimal LQ estimator gain K for the dynamical system:
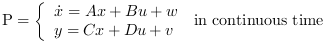
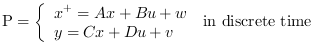
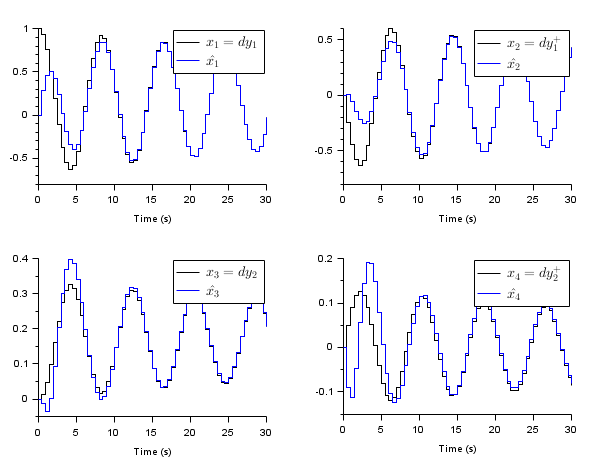
Where 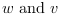 are white noises such
as
are white noises such
as 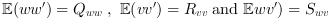
 | CautionThe values of |
 | Standard form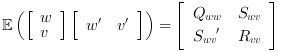 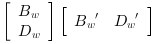 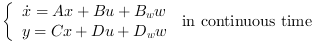 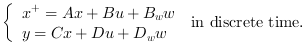 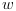 is now a white noise such
as is now a white noise such
as 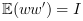 |
Syntax [K,X]=lqe(Pw)
Computes the linear optimal LQ estimator gain K for the dynamical system
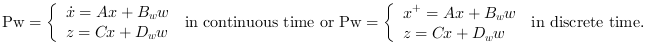
Where 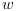 is a white noise with unit covariance.
is a white noise with unit covariance.
Properties
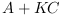 is stable.
is stable.the state estimator is given by the dynamical system:
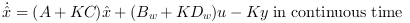
or
It minimizes the covariance of the steady state error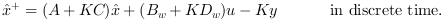
 .
.For discrete time systems the state estimator is such that:
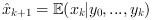 (one-step predicted
(one-step predicted 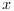 ).
).
Algorithm
let 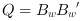 ,
, 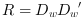 and
and 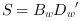
For the continuous time case K is given by
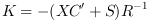
where
Xis the solution of the stabilizing Riccati equation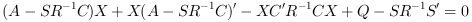
For the discrete time case K is given by
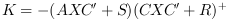
where
Xis the solution of the stabilizing Riccati equation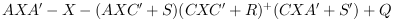
Examples
Assume the dynamical system formed by two masses connected by a spring and a damper:
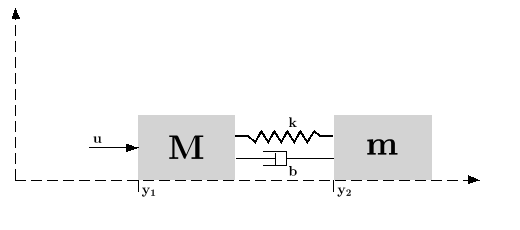
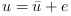 (where
(where 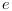 is a noise) is applied to the big one, the deviations from equilibrium positions
is a noise) is applied to the big one, the deviations from equilibrium positions 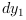 and
and 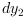 of the masses are measured. These measures are also subject to an additionnal noise
of the masses are measured. These measures are also subject to an additionnal noise 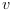 .
.
A continuous time state space representation of this system is:
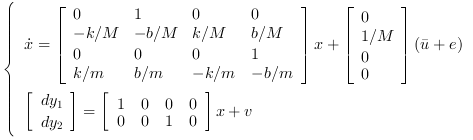
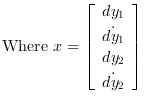
 and
and  are discrete time white noises such as
are discrete time white noises such as
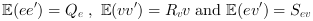
The instructions below can be used to compute a LQ state observer of the discretized version of this dynamical system.
// Form the state space model M = 1; m = 0.2; k = 0.1; b = 0.004; A = [ 0 1 0 0 -k/M -b/M k/M b/M 0 0 0 1 k/m b/m -k/m -b/m]; B = [0; 1/M; 0; 0]; C = [1 0 0 0 //dy1 0 0 1 0];//dy2 //inputs u and e; outputs dy1 and dy2 P = syslin("c",A, B, C); // Discretize it dt=0.5; Pd=dscr(P, dt); // Set the noise covariance matrices Q_e=0.01; //additive input noise variance R_vv=0.001*eye(2,2); //measurement noise variance Q_ww=Pd.B*Q_e*Pd.B'; //input noise adds to regular input u //----syntax [K,X]=lqe(P,Qww,Rvv [,Swv])--- Ko=lqe(Pd,Q_ww,R_vv); //observer gain //----syntax [K,X]=lqe(P21)--- bigR =sysdiag(Q_ww, R_vv); [W,Wt]=fullrf(bigR); Bw=W(1:size(Pd.B,1),:); Dw=W(($+1-size(Pd.C,1)):$,:); Pw=syslin(Pd.dt,Pd.A,Bw,Pd.C,Dw); Ko1=lqe(Pw); //same observer gain //Check gains equality norm(Ko-Ko1,1) // Form the observer O=observer(Pd,Ko); //check stability and(abs(spec(O.A))<1) // Check by simulation // Modify Pd to make it return the state Pdx=Pd;Pdx.C=eye(4,4);Pdx.D=zeros(4,1); t=0:dt:30; u=zeros(t); x=flts(u,Pdx,[1;0;0;0]);//state evolution y=Pd.C*x; // simulate the observer x_hat=flts([u+0.01*rand(u);y+0.0001*rand(y)],O); clf; subplot(2,2,1) plot2d(t',[x(1,:);x_hat(1,:)]'), e=gce();e.children.polyline_style=2; L=legend('$x_1=dy_1$', '$\hat{x_1}$');L.font_size=3; xlabel('Time (s)') subplot(2,2,2) plot2d(t',[x(2,:);x_hat(2,:)]') e=gce();e.children.polyline_style=2; L=legend('$x_2=dy_1^+$', '$\hat{x_2}$');L.font_size=3; xlabel('Time (s)') subplot(2,2,3) plot2d(t',[x(3,:);x_hat(3,:)]') e=gce();e.children.polyline_style=2; L=legend('$x_3=dy_2$', '$\hat{x_3}$');L.font_size=3; xlabel('Time (s)') subplot(2,2,4) plot2d(t',[x(4,:);x_hat(4,:)]') e=gce();e.children.polyline_style=2; L=legend('$x_4=dy_2^+$', '$\hat{x_4}$');L.font_size=3; xlabel('Time (s)')
Reference
Engineering and Scientific Computing with Scilab, Claude Gomez and al.,Springer Science+Business Media, LLC,1999, ISNB:978-1-4612-7204-5
See also
| Report an issue | ||
| << leqr | Linear Quadratic | lqg >> |