Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
interp
cubic spline evaluation function
Calling Sequence
[ yp [,yp1 [,yp2 [,yp3]]]] = interp(xp, x, y, d [, out_mode])
Arguments
- x,y
real vectors of same size
n: Coordinates of data points on which the interpolation and the related cubic spline (calleds(X)in the following) or sub-spline function is based and built.- d
real vector of size(x): The derivative s'(x). Most often, s'(x) will be priorly estimated through the function splin(x, y,..)
- out_mode
(optional) string defining
s(X)forXoutside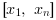 .
Possible values: "by_zero" | "by_nan" | "C0" | "natural" | "linear" | "periodic"
.
Possible values: "by_zero" | "by_nan" | "C0" | "natural" | "linear" | "periodic"- xp
real vector or matrix: abscissae at which
Yis unknown and must be estimated withs(xp)- yp
vector or matrix of size(xp):
yp(i) = s(xp(i))oryp(i,j) = s(xp(i,j))- yp1, yp2, yp3
vectors (or matrices) of size(x): elementwise evaluation of the derivatives
s'(xp),s''(xp)ands'''(xp).
Description
The cubic spline function s(X) interpolating the (x,y) set of given points is a continuous and derivable piece-wise function defined over 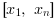 . It consists of a set of cubic polynomials, each one
. It consists of a set of cubic polynomials, each one 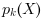 being defined on
being defined on  and connected in values and slopes to both its neighbours. Thus, we can state that for each
and connected in values and slopes to both its neighbours. Thus, we can state that for each 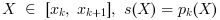 , such that
, such that
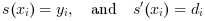 . Then, interp() evaluates
. Then, interp() evaluates s(X) (and s'(X), s''(X), s'''(X) if needed) at xp(i), such that
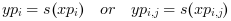
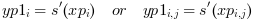
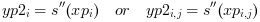
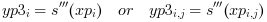
The out_mode parameter set the evaluation rule
for extrapolation, i.e. for xp(i) outside 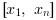 :
:
- "by_zero"
an extrapolation by zero is done
- "by_nan"
extrapolation by Nan (%nan)
- "C0"
the extrapolation is defined as follows :
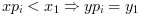
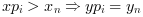
- "natural"
the extrapolation is defined as follows (
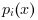 being the polynomial defining
being the polynomial defining
s(X)on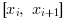 )
)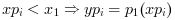
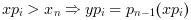
- "linear"
the extrapolation is defined as follows :
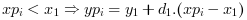
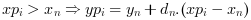
- "periodic"
s(X)is extended by periodicity: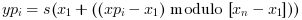
Examples
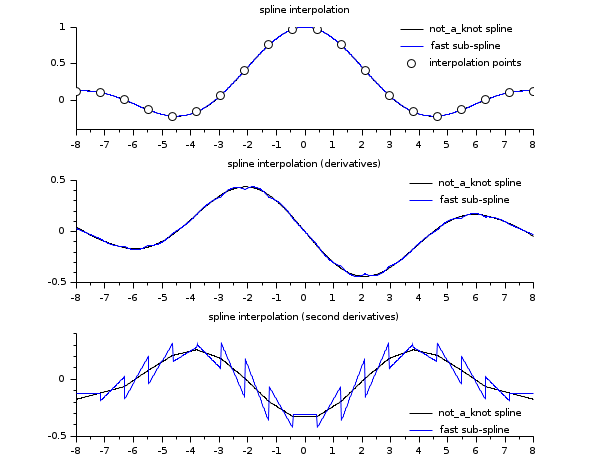
// see the examples of splin and lsq_splin // an example showing C2 and C1 continuity of spline and subspline a = -8; b = 8; x = linspace(a,b,20)'; y = sinc(x); dk = splin(x,y); // not_a_knot df = splin(x,y, "fast"); xx = linspace(a,b,800)'; [yyk, yy1k, yy2k] = interp(xx, x, y, dk); [yyf, yy1f, yy2f] = interp(xx, x, y, df); clf() subplot(3,1,1) plot2d(xx, [yyk yyf]) plot2d(x, y, style=-9) legends(["not_a_knot spline","fast sub-spline","interpolation points"],... [1 2 -9], "ur",%f) xtitle("spline interpolation") subplot(3,1,2) plot2d(xx, [yy1k yy1f]) legends(["not_a_knot spline","fast sub-spline"], [1 2], "ur",%f) xtitle("spline interpolation (derivatives)") subplot(3,1,3) plot2d(xx, [yy2k yy2f]) legends(["not_a_knot spline","fast sub-spline"], [1 2], "lr",%f) xtitle("spline interpolation (second derivatives)")
// here is an example showing the different extrapolation possibilities x = linspace(0,1,11)'; y = cosh(x-0.5); d = splin(x,y); xx = linspace(-0.5,1.5,401)'; yy0 = interp(xx,x,y,d,"C0"); yy1 = interp(xx,x,y,d,"linear"); yy2 = interp(xx,x,y,d,"natural"); yy3 = interp(xx,x,y,d,"periodic"); clf() plot2d(xx,[yy0 yy1 yy2 yy3],style=2:5,frameflag=2,leg="C0@linear@natural@periodic") xtitle(" different way to evaluate a spline outside its domain")

History
| Version | Description |
| 5.4.0 | previously, imaginary part of input arguments were implicitly ignored. |
| Report an issue | ||
| << eval_cshep2d | Interpolation | interp1 >> |