- Scilab help
- Statistics
- cdfbet
- cdfbin
- cdfchi
- cdfchn
- cdff
- cdffnc
- cdfgam
- cdfnbn
- cdfnor
- cdfpoi
- cdft
- center
- wcenter
- cmoment
- correl
- covar
- ftest
- ftuneq
- geomean
- harmean
- iqr
- mad
- mean
- meanf
- median
- moment
- msd
- mvvacov
- nancumsum
- nand2mean
- nanmax
- nanmean
- nanmeanf
- nanmedian
- nanmin
- nanstdev
- nansum
- nfreq
- pca
- perctl
- princomp
- quart
- regress
- sample
- samplef
- samwr
- show_pca
- st_deviation
- stdevf
- strange
- tabul
- thrownan
- trimmean
- variance
- variancef
Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
cdfnor
cumulative distribution function normal distribution
Calling Sequence
[P,Q]=cdfnor("PQ",X,Mean,Std) X=cdfnor("X",Mean,Std,P,Q) Mean=cdfnor("Mean",Std,P,Q,X) Std=cdfnor("Std",P,Q,X,Mean)
Arguments
- P,Q,X,Mean,Std
matrix of doubles of the same size.
- P,Q (Q=1-P)
The integral from -infinity to X of the normal density. Input range: (0,1].
- X
Upper limit of integration of the normal-density. Input range: ( -infinity, +infinity)
- Mean
The mean of the normal density. Input range: (-infinity, +infinity)
- Sd
Standard Deviation of the normal density. Input range: (0, +infinity).
Description
Calculates any one parameter of the normal distribution given values for the others.
A slightly modified version of ANORM from Cody, W.D. (1993). "ALGORITHM 715: SPECFUN - A Portabel FORTRAN Package of Special Function Routines and Test Drivers" acm Transactions on Mathematical Software. 19, 22-32. is used to calulate the cumulative standard normal distribution.
The rational functions from pages 90-95 of Kennedy and Gentle, Statistical Computing, Marcel Dekker, NY, 1980 are used as starting values to Newton's Iterations which compute the inverse standard normal. Therefore no searches are necessary for any parameter.
For X < -15, the asymptotic expansion for the normal is used as the starting value in finding the inverse standard normal. This is formula 26.2.12 of Abramowitz and Stegun.
The cumulated distribution function definition is:
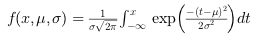
From DCDFLIB: Library of Fortran Routines for Cumulative Distribution Functions, Inverses, and Other Parameters (February, 1994) Barry W. Brown, James Lovato and Kathy Russell. The University of Texas.
Examples
// Compute p from x x = -1; Mean = 0; Std = 1; // P = 0.1586553, Q = 0.8413447 [P,Q]=cdfnor("PQ",x,Mean,Std) // Compute p from a very rare x // Notice that Q should be used when P is close to 1, // while P should be used when Q is close to 1. x = 10; Mean = 0; Std = 1; // P = 1, Q = 7.620D-24 [P,Q]=cdfnor("PQ",x,Mean,Std) // Make a table of P,Q Mean = 0; Std = 1; x = -6:6; [P,Q]=cdfnor("PQ",x,Mean*ones(x),Std*ones(x)); [x' P' Q'] // Find x from p,q Mean = 0; Std = 1; p = 0.1; q = 0.9; // x = - 1.2815516 x = cdfnor("X",Mean,Std,p,q) // Find Mean from p,q x = 2; Std = 1; p = 0.1; q = 0.9; // Mean = 3.2815516 Mean = cdfnor("Mean",Std,p,q,x) // Find Standard Deviation from p,q Mean = 0; p = 0.1; q = 0.9; x = 2; // Std = - 1.5606083 Std = cdfnor("Std",p,q,x,Mean) // Plot the function h = scf(); Mean = [0 0 0 -2]; Std2 = [0.2 1.0 5.0 0.5]; cols = [1 2 3 4]; nf = size(cols,"*"); lgd = []; for k = 1 : nf x = linspace(-5,5,1000); P=cdfnor("PQ",x,Mean(k)*ones(x),sqrt(Std2(k))*ones(x)); plot(x,P) str = msprintf("Mean=%s, Std^2=%s",string(Mean(k)),string(Std2(k))); lgd($+1) = str; end for k = 1 : nf h.children.children.children(nf - k + 1).foreground = cols(k); end legend(lgd); // Plot the Inverse Cumulated Standard function Mean = 0; Std = 1; p = linspace(1e-10,1-1e-10,1000); q = 1-p; x = cdfnor("X",Mean*ones(p),Std*ones(p),p,q); plot(p,x) xtitle("Inverse Cumulated Distribution Normal Standard Function","p","x"); // The Inverse Normal CDF is ill-conditionned when // p is close to p=0.5. // This is because, at p=0.5, the first derivative is non-zero, // while the function is zero. // This may produce a large relative error in the function value, // that is, some digits may not be accurate when p is getting // closer and closer to p=0.5. Mean = 0; Std = 1; p = 0.500000001; q = 1-p; x = cdfnor("X",Mean,Std,p,q) // The expected probability was computed from a symbolic software, // with the expression sqrt(2)*erfinv(2*p-1) // where p = 1/2+10^-9. expected = 2.50662827463100050e-9; // The relative error is about 1.e-8, meaning that // only 8 digits are accurate. abs(x-expected)/abs(expected) // The zero-finder algorithm may be unable to find the standard // deviation in some situations when the inversion cannot be // performed. Mean = 1; p = 0.5; q = 0.5; x = 1; // Std = Nan Std = cdfnor("Std",p,q,x,Mean)
| << cdfnbn | Statistics | cdfpoi >> |