contourf
filled level curves of a surface on a 2D plot
Syntax
contourf(x, y, z, nz, [style, strf, leg, rect, nax, fpf])
Arguments
- x, y
two real row vectors of size
n1andn2: the grid.- z
a real matrix of size
(n1,n2), the values of the function.- nz
the level values or the number of levels.
- -
If
nzis an integer, its value gives the number of level curves equally spaced fromzmintozmaxas follows:z= zmin + (1:nz)*(zmax-zmin)/(nz+1)
 Note: that the
Note: that thezminandzmaxlevels are not drawn (generically they are reduced to points) but they can be added with- -
If
nzis a vector,nz(i)gives the value of thei-th level curve.
- style, strf, leg, rect, nax
see
plot2d. The argumentstylegives the colors which are to be used for level curves. It must have the same size as the number of levels.- fpf
You can change the format of the floating point number printed on the levels where
fpfis the format in C format syntax (for examplefpf="%.3f"). Setfpfto " " implies that the level are not drawn on the level curves. If not given, the default format of contour2d is used.
Description
contourf paints surface between two consecutive
level curves of a surface z=f(x,y) on a 2D plot.
The values of f(x,y) are given by the matrix
z at the grid points defined by
x and y.
Enter the command contourf() to see a demo.
Examples
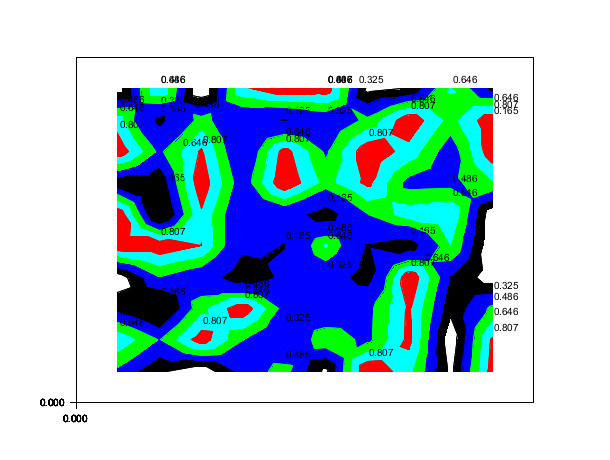
contourf(1:10,1:10,rand(10,10),5,1:5,"011"," ",[0,0,11,11])
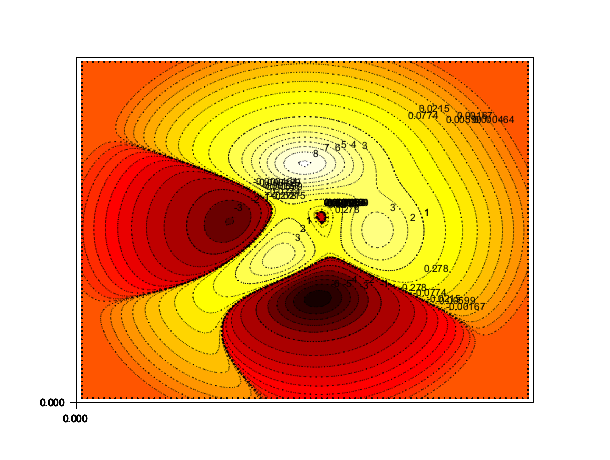
z = peaks(-4:0.1:4); levels = [-6:-1,-logspace(-5,0,10),logspace(-5,0,10),1:8]; m = size(levels,'*'); n = fix(3/8*m); r = [(1:n)'/n; ones(m-n,1)]; g = [zeros(n,1); (1:n)'/n; ones(m-2*n,1)]; b = [zeros(2*n,1); (1:m-2*n)'/(m-2*n)]; h = [r g b]; gcf().color_map = h; clf(); contourf([],[],z',levels,zeros(1,m));
See also
- contour — level curves on a 3D surface
- contour2d — level curves of a surface on a 2D plot
- contour2di — compute level curves of a surface on a 2D plot
- plot2d — 2D plot
| Report an issue | ||
| << contour2dm | 2d_plot | cutaxes >> |