Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
blockdiag
Создаёт блочную диагональную матрицу из указанных массивов. Соединение диагональной системы блоков.
Синтаксис
r = blockdiag(a1,a2,...,an)
Аргументы
- ai
Матрицы логических значений, чисел, полиномов, рациональных или строковых значений любого размера. Принимаются разрежённые матрицы.
Подсистемы (т.е. коэффициенты усиления, или линейные системы в пространстве состояний или передаточной форме).
- r
Матрица с
a1, a2, a3, ... по диагонали.rявляется разрежённой, хотя бы одна из входныхaiразрёжённая.
Описание
Подав на вход A, B and C,
на выходе эти матрицы будут расставлены по диагонали:
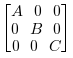
Если все входные матрицы квадратные, то выходная матрицы известна как блочная диагональная матрица block diagonal matrix.
Если указаны подсистемы, то blockdiag(..) выдаёт блочно-
диагональную систему, сделанную из подсистем, располженых на главной диагонали.
Это может быть использовано в частности для соединений системы.
 | blockdiag() может быть перегружена. |
Примеры
С числами:
A = [1 0 ; 0 1] B = [3 4 5 ; 6 7 8] C = 7 D = blockdiag(A, B, C)
--> D = blockdiag(A, B, C) D = 1. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 3. 4. 5. 0. 0. 0. 6. 7. 8. 0. 0. 0. 0. 0. 0. 7.
С логическими значениями:
blockdiag([%T %T %T], [%T ; %F], [%T %F])
--> blockdiag([%T %T %T], [%T ; %F], [%T %F]) ans = T T T F F F F F F T F F F F F F F F F F F F T F
С полиномами:
s = %s; blockdiag(s, [s^2 ; s^3], [1+s, 1-s^2 ; 4 s^4])
--> b = blockdiag(s, [s^2 ; s^3], [1+s, 1-s^2 ; 4 s^4])
b =
s 0 0 0
2
0 s 0 0
3
0 s 0 0
2
0 0 1 +s 1 -s
4
0 0 4 s
С рациональными значениями:
s = %s; blockdiag([1/s 2*s/(4*s+3)], 1/(s-1)^2)
--> blockdiag([1/s 2*s/(4*s+3)], 1/(s-1)^2)
ans =
1 2s 0
-- ------- --
s 3 + 4s 1
0 0 1
-- -- -----------
2
1 1 1 - 2s + s
С некоторыми разрежёнными матрицами на входе:
--> S = blockdiag([1 2], sparse([0 3 ; 4 0]), 5) S = ( 4, 5) sparse matrix ( 1, 1) 1. ( 1, 2) 2. ( 2, 4) 3. ( 3, 3) 4. ( 4, 5) 5. --> full(S) ans = 1. 2. 0. 0. 0. 0. 0. 0. 3. 0. 0. 0. 4. 0. 0. 0. 0. 0. 0. 5.
С текстом:
blockdiag(["Scilab" "is"],"a",["scientific" ; "software"])
--> blockdiag(["Scilab" "is"], "a", ["scientific" ; "software"]) ans = !Scilab is ! ! a ! ! scientific ! ! software !
Со смешанными конкатенируемыми типами данных (см. справку по квадратным скобкам
[]):
blockdiag([%T %F], [-1 3], (1-%z)^2)
--> blockdiag([%T %F], [-1 3], (1-%z)^2)
ans =
1 0 0 0 0
0 0 -1 3 0
2
0 0 0 0 1 -2z +z
С линейной системой:
Смотрите также
История
| Версия | Описание |
| 6.1.0 | Введена blockdiag(). |
| Report an issue | ||
| << random | Элементарные матрицы | diag >> |