- Aide de Scilab
- Traitement du Signal
- Filtrage
- How to design an elliptic filter
- analpf
- buttmag
- casc
- cheb1mag
- cheb2mag
- ell1mag
- eqfir
- eqiir
- faurre
- ffilt
- filt_sinc
- filter
- find_freq
- frmag
- fsfirlin
- group
- hilbert
- iir
- iirgroup
- iirlp
- kalm
- lev
- levin
- lindquist
- remez
- remezb
- sgolay
- sgolaydiff
- sgolayfilt
- srfaur
- srkf
- sskf
- syredi
- system
- trans
- wfir
- wfir_gui
- wiener
- wigner
- window
- yulewalk
- zpbutt
- zpch1
- zpch2
- zpell
Please note that the recommended version of Scilab is 2026.0.0. This page might be outdated.
See the recommended documentation of this function
sgolaydiff
Numerical derivatives computation using Savitzky-Golay filter.
Syntax
D = sgolaydiff(X, order, k, nf) D = sgolaydiff(X, order, k, nf, w) D = sgolaydiff(X, order, C)
Arguments
- X
It can be either a real vector or a general real array. If it is an array the derivation is applied along the first non singleton dimension.
- order
a positive scalar with integer value, the order of derivation.
- C
a real nf by k+1 array: the matrix of differentiation filters computed by the sgolay function.
- k
a positive scalar with integer value: the fitting polynomial degree.
- nf
a positive scalar with integer value: the filter length, must be odd and greater the k+1.
- w
a real vector of length nf with positive entries: the weights. If omitted no weights are applied.
- D
A vector with identical shape as X, the estimated derivative.
Description
This function computes numerical derivatives using the FIR Savitzky-Golay smoothing Filter. This is achieved by fitting successive sub-sets of adjacent data points with a low-degree polynomial by the method of linear least squares.
 | order must be less than k |
 | The (nf−1)/2 first and last derivative values are estimated by adding to the input signal, in reverse order and vertically symmetrized, copies of the first (nf−1)/2 points at the beginning and copies of the last (nf−1)/2 points at the end . |
Examples
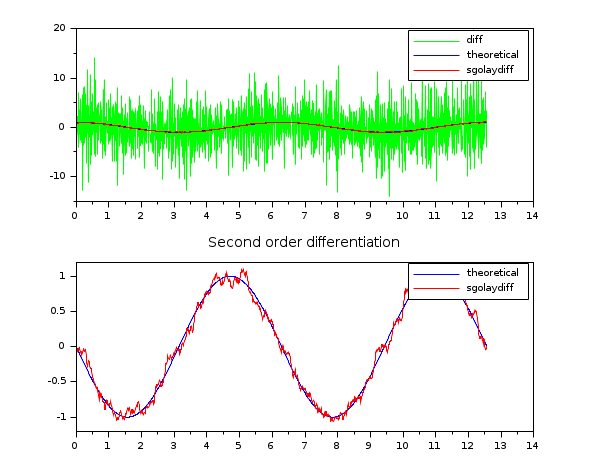
//generate a noisy signal dt=0.01; t = (0:0.01:4*%pi)'; x = sin(t)+0.03*rand(t,"normal"); clf(); //first order derivative subplot(211) dx = sgolaydiff(x,1,3,61); plot(t(2:$),diff(x)/dt,'g',t,cos(t),'b',t,dx/dt,'r'); legend(["diff","theoretical","sgolaydiff"]); //second order derivative subplot(212) d2x = sgolaydiff(x,2,3,101); plot(t,-sin(t),'b',t,d2x/(dt^2),'r'); legend(["theoretical","sgolaydiff"]); title("Second order differentiation")
Bibliography
Abraham Savitzky et Marcel J. E. Golay, « Smoothing and Differentiation of Data by Simplified Least Squares Procedures », Analytical Chemistry, vol. 8, no 36, 1964, p. 1627–1639 (DOI 10.1021/ac60214a047)
See Also
- sgolay — Savitzky-Golay Filter Design
- sgolayfilt — Filter signal using Savitzky-Golay Filter.
- diff — Difference and discrete derivative
History
| Version | Description |
| 6.1.1 | Function added. Courtesy of Serge Steer, INRIA |
| Report an issue | ||
| << sgolay | Filtrage | sgolayfilt >> |