qld

Arguments

Q

real positive definite symmetric matrix (dimension n x n ).

p

real (column) vector (dimension n)

C

real matrix (dimension (me + md) x n )

b

RHS column vector (dimension (me + md) )

ci

column vector of lower-bounds (dimension n). If there are no lower bound constraints, put ci = []. If some components of x are bounded from below, set the other (unconstrained) values of ci to a very large negative number (e.g. ci(j) = -number_properties('huge') .

cs

column vector of upper-bounds. (Same remarks as above).

me

number of equality constraints (i.e. C(1:me,:)*x = b(1:me) )

tol

Floating point number, required precision.

x

optimal solution found.

lagr

vector of Lagrange multipliers.

If lower and upper-bounds ci, cs are provided, lagr has me + md + 2* n components. The components lagr(1:me + md) are associated with the linear constraints and lagr (me + md + 1 : 2 * n) are associated with the lower and upper bounds constraints.

If an upper-bound (resp. lower-bound) constraint i is active lagr(i) is > 0 (resp. <0). If no bounds are provided, lagr has only me + md components.

On successful termination, all values of lagr with respect to inequalities and bounds should be greater or equal to zero.

info

integer, return the execution status instead of sending errors.

info==1 : Too many iterations needed

info==2 : Accuracy insufficient to satisfy convergence criterion

info==5 : Length of working array is too short

info==10: The constraints are inconsistent

Description

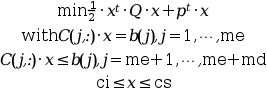
This function requires Q to be positive definite, if it is not the case, one may use the contributed toolbox "quapro".

Examples

//Find x in R^6 such that:
//C1*x = b1 (3 equality constraints i.e me=3)
C1= [1,-1,1,0,3,1;
    -1,0,-3,-4,5,6;
     2,5,3,0,1,0];
b1=[1;2;3];

//C2*x <= b2 (2 inequality constraints i.e md=2)
C2=[0,1,0,1,2,-1;
    -1,0,2,1,1,0];
b2=[-1;2.5];

//with  x between ci and cs:
ci=[-1000;-10000;0;-1000;-1000;-1000];cs=[10000;100;1.5;100;100;1000];

//and minimize 0.5*x'*Q*x + p'*x with
p=[1;2;3;4;5;6]; Q=eye(6,6);

//No initial point is given;
C=[C1;C2];
b=[b1;b2];
me=3;
[x,lagr]=qld(Q,p,C,b,ci,cs,me)
//Only linear constraints (1 to 4) are active (lagr(1:6)=0):

See also

• qpsolve — linear quadratic programming solver
• optim — non-linear optimization routine

The contributed toolbox "quapro" may also be of interest, in particular for singular Q.

Used Functions

ql0001.f in modules/optimization/src/fortran/ql0001.f