Please note that the recommended version of Scilab is 2026.0.1. This page might be outdated.
See the recommended documentation of this function
lqg
LQG compensator
Syntax
K = lqg(P_aug, r) K = lqg(P, Qxu, Qwv) K = lqg(P, Qxu, Qwv, Qi, #dof)
Arguments
- P_aug
State space representation of the augmented plant (see: lqg2stan)
- r
1 by 2 row vector = (number of measurements, number of inputs) (dimension of the 2,2 part of
P_aug)- P
State-space representation of the nominal plant (
nuinputs,nyoutputs,nxstates).- Qxu
Symmetric
nx+nubynx+nuweighting matrix.- Qwv
Symmetric
nx+nybynx+nycovariance matrix.- Qi
Symmetric
nybynyweight for integral term.- #dof
Scalar with value in {1,2}, the degrees of freedom of the controller. The default value is 2.
- K
Linear LQG (H2) controller in state-space representation.
Description
Regulation around zero
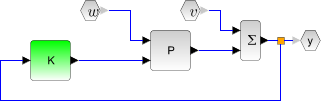
- Syntax
K=lqg(P_aug,r)Computes the linear optimal LQG (H2) controller for the "augmented" plant
P_augwhich can be generated by lqg2stan givent the nominal plant plantP, the weighting matrixQxuand the noise covariance matrixQwv. - Syntax
K=lqg(P,Qxu,Qwv)Computes the linear optimal LQG (H2) controller for the nominal plant
P, the weighting matrixQxuand the noise covariance matrixQwv
Regulation around a reference signal, Syntax K=lqg(P,Qxu,Qwv,Qi [,#dof])
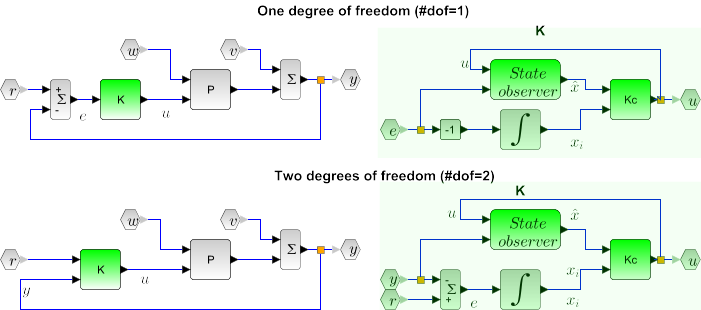
Computes the linear optimal LQG (H2) reference tracking controller for the
plant P, the weighting matrix
Qxu and the noise covariance matrix
Qwv
Examples
Assume the dynamical system formed by two masses connected by a spring and a damper:
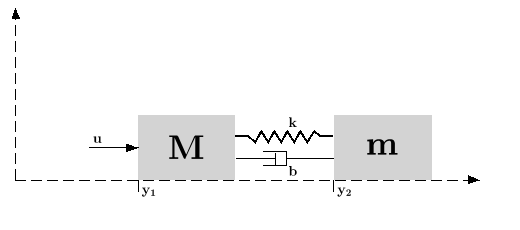
A force 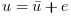 (where e is a noise) is
applied to M, the deviations dy1 and
dy2 from equilibrium positions of the
masses are measured. These measures are subject to an additional
noise v.
(where e is a noise) is
applied to M, the deviations dy1 and
dy2 from equilibrium positions of the
masses are measured. These measures are subject to an additional
noise v.
A continuous time state space representation of this system is:
![\left\lbrace\begin{array}{l}
\dot{x}=\left[\begin{array}{llll}0&1&0&0\\ -k/M&-b/M&k/M&b/M\\
0&0&0&1\\ k/m&b/m&-k/m&-b/m \end{array}\right] x
+\left[\begin{array}{l}0\\ 1/M\\ 0\\ 0 \end{array}\right]
(\bar{u}+e)\\ \left[\begin{array}{l}dy_1\\
dy_2\end{array}\right]=\left[\begin{array}{llll}1&0&0&0\\
0&0&1&0 \end{array}\right] x +v \end{array}\right.](/docs/6.1.1/en_US/_LaTeX_lqg.xml_2.png)
![\text{Where }x=\left[\begin{array}{l}dy_1\\ \dot{dy_1}\\ dy_2\\
\dot{dy_2}\end{array}\right]](/docs/6.1.1/en_US/_LaTeX_lqg.xml_3.png)
The instructions below can be used to compute a LQG compensator of the discretized version of this dynamical system. e and v are discrete time white noises such as
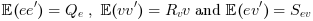
The LQ cost is defined by
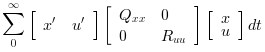
Regulation around zero
// Form the state space model M = 1; m = 0.2; k = 0.1; b = 0.004; A = [0 1 0 0 -k/M -b/M k/M b/M 0 0 0 1 k/m b/m -k/m -b/m]; B = [0; 1/M; 0; 0]; C = [1 0 0 0 //dy1 0 0 1 0];//dy2 //inputs u and e; outputs dy1 and dy2 P = syslin("c",A, B, C); // Discretize it dt=0.5; Pd=dscr(P, dt); // The noise variances Q_e=1; //additive input noise variance R_vv=0.0001*eye(2,2); //measurement noise variance Q_ww=Pd.B*Q_e*Pd.B'; //input noise adds to regular input u Qwv=blockdiag(Q_ww,R_vv); //The compensator weights Q_xx=diag([0.1 0 5 0]); //Weights on states R_uu = 0.3; //Weight on input Qxu=blockdiag(Q_xx,R_uu); //----syntax [K,X]=lqg(P,Qxu,Qwv)--- J=lqg(Pd,Qxu,Qwv); //----syntax [K,X]=lqg(P_aug,r)--- // Form standard LQG model [Paug,r]=lqg2stan(Pd,Qxu,Qwv); // Form standard LQG model J1=lqg(Paug,r); // Form the closed loop Sys=Pd/.(-J); // Compare real and Estimated states for initial state evolution t = 0:dt:30; // Simulate system evolution for initial state [1;0;0;0; y = flts(zeros(t),Sys,eye(8,1)); clf; plot2d(t',y') e=gce();e.children.polyline_style=2; L=legend(["$dy_1$","$dy_2$"]);L.font_size=4; xlabel('Time (s)')
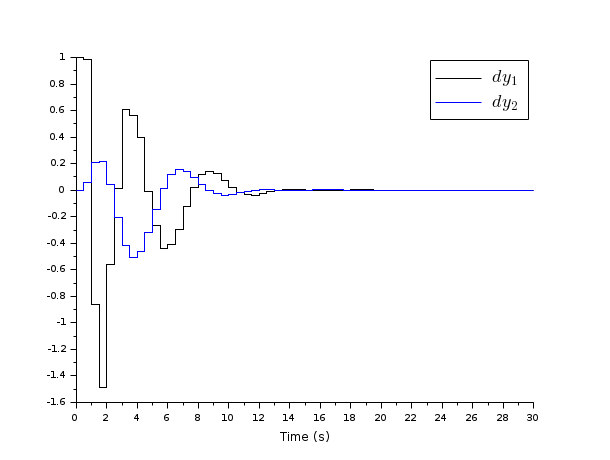
Regulation around a reference signal, Syntax K=lqg(P,Qxu,Qwv,Qi [,#dof])
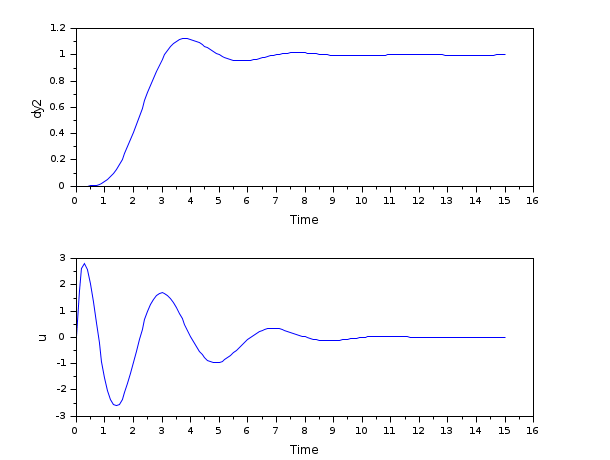
The purpose of the controller is here to assign dy2 using the measure of dy2.
M = 1; m = 0.2; k = 0.1; b = 0.004; A = [0 1 0 0 -k/M -b/M k/M b/M 0 0 0 1 k/m b/m -k/m -b/m]; B = [0; 1/M; 0; 0]; C = [1 0 0 0 //dy1 0 0 1 0];//dy2 //inputs u and e; outputs dy1 and dy2 P = syslin("c",A, B, C); // Discretize it dt=0.1; Pd=dscr(P, dt); // The noise variances Q_e=1; //additive input noise variance R_vv=0.0001; //measurement noise variance Q_ww=Pd.B*Q_e*Pd.B'; //input noise adds to regular input u Qwv=blockdiag(Q_ww,R_vv); //The compensator weights Q_xx=diag([0.1 0 1 0]); //Weights on states R_uu = 0.1; //Weight on input Qxu=blockdiag(Q_xx,R_uu); //Control of the second mass position (y2) Qi=50; J=lqg(Pd(2,:),Qxu,Qwv,Qi); H=lft([1;1]*Pd(2,:)*(-J),1); //step response t=0:dt:15; r=ones(t); dy2=flts(r,H); clf; subplot(211);plot(t',dy2');xlabel("Time");ylabel("dy2") u=flts([r;dy2],J); subplot(212);plot(t',u');xlabel("Time");ylabel("u")
Reference
Engineering and Scientific Computing with Scilab, Claude Gomez and al.,Springer Science+Business Media, LLC,1999, ISNB:978-1-4612-7204-5
See Also
History
| Version | Description |
| 6.0 | lqg(P,Qxu,Qwv) and lqg(P,Qxu,Qwv,Qi,#dof) syntaxes added. |
| Report an issue | ||
| << lqe | Linear Quadratic | lqg2stan >> |